Упражнения

4.1. Найти число ребер и степени вершин в полных графах К₆, К₇, К₈.

4.2. Найти количество ребер в полных двудольных графах К_{4, 6}, К_{3, 5}, К_{2, 3}. Составить матрицу связности графа К_{2, 3}.

4.3. Найти количество ребер в графах Е², Е³, Е⁴. Построить реализации графов Е², Е³ (Е², Е³, Е⁴ – двух-, трех-, четырехмерные кубы).

4.4. Найти число полных трехвершинных подграфов в полных двудольных графах К_{3, 5}, К_{4, 3}.

4.5. Количество ребер в однородном графе G равно 15. Степень каждой вершины графа равна 3. Найти количество вершин графа G.

4.6. Существует ли полный граф с семью ребрами? С 50 ребрами?

4.7. Дан полный граф G и "_i: δ (v _i) = 20. Найти количество вершин и ребер графа.

4.8. Доказать, что графы Е³, Е⁴ являются двудольными.

4.9. Найти дополнение графа G до полного графа. Составить матрицы смежности графа G и его дополнения (по формуле).

G:

4.10. Для заданного графа G:

а) Построить соответствующий реберный граф;

б) Найти матрицу смежности реберного графа через матрицу инцидентности исходного графа (по формуле);

в) Определить степени вершин реберного графа через степени вершин исходного графа;

г) Определить число ребер в реберном графе, используя исходный граф G:

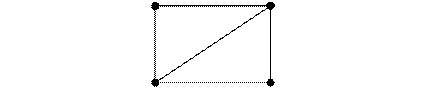
4.11. Построить однородный 5-вершинный граф. Составить его матрицу инцидентности. По матрице инцидентности найти матрицу смежности однородного графа. Построить соответствующий реберный граф. Найти его матрицу смежности, степени вершин, число ребер, используя исходный однородный граф.