Сначала давайте поймем, как будут накапливаться деньги. Через год на счету вкладчика будет сумма:10 000 + 10 000´ 
(руб.), т.е. исходная сумма плюс проценты. Еще через год эта сумма составит 
(руб.), т.е. сумма денег после первого года и проценты от денег первого года. Ясно, что дальше все будет происходить по этой же схеме, однако не складывать же нам все эти суммы до тех пор, пока не получим сумму в 20 000 руб.!
Попробуем найти закон образования суммы вклада после каждого года.
После первого года: 
.
После второго года: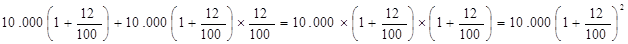 
После третьего года: 
Внимательно присмотревшись к правым частям наших равенств, можно заметить закономерность построения этих денежных сумм и увидеть, что через n лет хранение денег их количество составит 
рублей. На самом деле мы сейчас вывели формулу, которая в экономике называется формулой сложных процентов: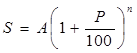 
, где A-начальная сумма вклада, P-процентная ставка (годовая), n-срок хранения вклада (в годах), а S-накопительная (итоговая) сумма вклада.
Итак, в нашем случае деньги на вкладе накапливаются по формуле 
. Нам необходимо найти n, при котором 
, т.е. решить уравнение 
.
Мы можем решить это уравнение по определению логарифма числа и получить, что n=log. Вычислим этот логарифм, предварительно перейдя к основанию 10, пользуясь калькулятором.
.
Таким образом, удвоение вклада произойдет через 6 лет (с небольшим).
