Нормальным называют распределение вероятностей непрерывной случайной величины, которое задается следующей функцией плотности:
Здесь а – математическое ожидание, а s – среднее квадратичное отклонение нормального распределения.
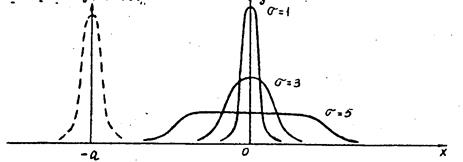
График дифференциальной функции нормального распределения называется нормальной кривой (кривой Гаусса). Форма кривой зависит от значений а и s.
Пaрамeтp а не изменяет форму кривой, a изменяет лишь ее расположение относительно оси У. При а>0 кривая сдвинута вправо, а при а<0 – влево. С возрастанием s максимальная ордината нормальной кривой убывает.
Пусть нормально распределенная случайная величина Х примет значение, принадлежащее интервалу (a, b). Вероятность этого события определяется формулой:
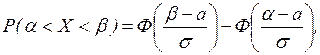
где Ф(x) – функция Лапласа – интегральная функция нормального распределения для случая 
и 
, т.е. центрированного и нормированного распределения.
Вероятность того, что отклонение нормально распределенной величины по абсолютной величине меньше заданного числа d определяется следующим образом:
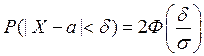
Правило трех сигм: P(|X-a|<3s) = 2Ф(3) = 2×0,49865 = 0,9973
