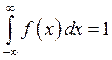Функцией распределения называют функцию F(х), определяющую вероятность того, что случайная величина X в результате испытания примет значение не большее х, т.е. F(x) = P(X< x).
Функцию распределения называют также интегральной функцией. Непрерывная случайная величина имеет непрерывную функцию распределения.
Свойства функции распределения.
1.Значение функции F(x) принадлежит интервалу [0;1]: 0£ F(x) £1 ,
2.F(x) – неубывающая функция, т.е. F(х2)³ (х1), если х2 > х1 ,
3. Если возможные значения случайной величины принадлежат интервалу (а, b), то F(х)=0 при х £ а , F(х)=1 при х ³ b.
Вероятность того, что случайная величина примет значение, принадлежащее интервалу (а, b) равна приращению функции распределения на этом интервале: Р(а<х<b) = F(b) – F(а).
Вероятность того, что непрерывная случайная величина X примет одно определенное значение, равна 0.
Плотностью распределения вероятностей непрерывной случайной величины (НCВ) называют функцию f(х) – первую производную от функции распределения:
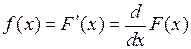
Вероятность того, что НСВ Х примет значение, принадлежащее интервалу (а, b), равна:
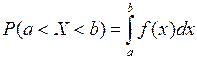
Если известна функция плотности распределения f(t), то функция распределения F(х) находится по формуле:
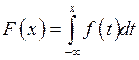
Свойства плотности распределения
1. f(х) является неотрицательной функцией f(x)³0,
2. Несобственным интеграл от плотности распределения равен 1: