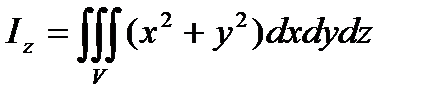В цилиндрических координатах положение точки M(x,y,z) в пространстве Oxyz определяется тремя числами − ρ, φ, z , где ρ − длина радиуса-вектора проекции точки M на плоскость Oxy, φ − угол, образованный этим радиусом-вектором с осью Ox (рисунок 1), z − проекция на ось Oz (ее значение одинаково в декартовых и цилиндрических координатах).
Цилиндрические координаты точки связаны с ее декартовыми координатами соотношениями
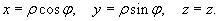
Здесь предполагается, что
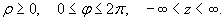
Тогда формула замены переменных при данном преобразовании имеет вид:
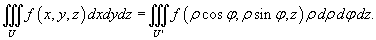
Переход к цилиндрическим координатам упрощает вычисление тройного интеграла в случаях, когда область интегрирования образована цилиндрической поверхностью.
46. Замена переменной в тройном интеграле: сферические координаты
Сферическими координатами точки M(x,y,z) называются три числа − ρ, φ, θ , где
ρ − длина радиуса-вектора точки M;
φ − угол, образованный проекцией радиуса-вектора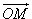 
на плоскость Oxy и осью Ox;
θ − угол отклонения радиуса-вектора 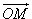от положительного направления оси Oz (рисунок 1).
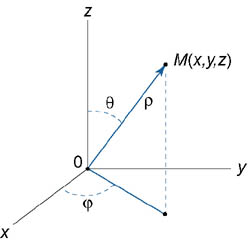
Сферические координаты точки связаны с ее декартовыми координатами соотношениями
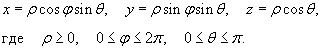Следовательно, формула замены переменных при преобразовании декартовых координат в сферические имеет вид:
| |
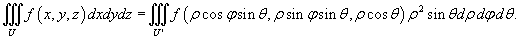
Приложения тройного интеграла
С помощью тройного интеграла можно вычислить:
1. Объем тела и его массу
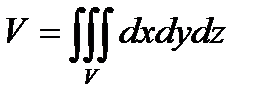
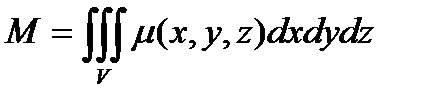, где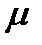 
- объемная плотность распределения массы
2. Момент инерции однородного тела относительно, например, оси Ох
