1.1. Пусть 
-неотрицательная, непрерывная функция в замкнутой области 
. Если 
- тело, ограниченное сверху поверхностью , снизу - областью , а сбоку - соответствующей цилиндрической поверхностью с образующей параллельной оси OZ и направляющей, совпадающей с границей области , то объем этого тела равен
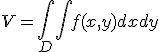
1.2. Пусть - тело, ограниченное сверху поверхностью , снизу - поверхностью 
, причем проекцией обеих поверхностей на плоскость 
служит область , в которой функции 
и 
непрерывны (и 
), то объем этого тела равен
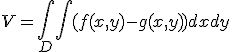
Приложения двойного интеграла
