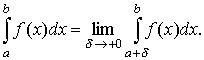Пусть функция y = f (x) непрерывна, но не ограниченая на полуинтервале [a, b).
Определение. Если существует и конечен предел
 ,
,
где δ > 0, то он называется несобственным интегралом (несобственным интегралом второго рода) от функции y = f (x) на [а, b) и обозначается  , т.е.
, т.е.
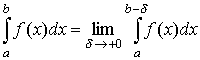
В этом случае данный несобственный интеграл (9.5) называется сходящимся, в противном случае — расходящимся.
Аналогично вводится понятие несобственного интеграла от функции y = f(x) непрерывной, но неограниченной на (а, b]: