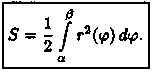1.Криволинейной трапецией называется плоская фигура, ограниченная осью 
, прямыми 
, 
и графиком непрерывной на отрезке 
функции 
, которая не меняет знак на этом промежутке. Пусть данная фигура расположена не ниже оси абсцисс:
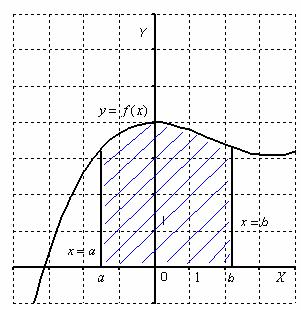
Тогда площадь криволинейной трапеции численно равна определенному интегралу
2.Если криволинейная трапеция расположенапод осью(или, по крайней мере, не выше данной оси), то её площадь можно найти по формуле: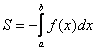 
3.Если на отрезке некоторая непрерывная функция 
больше либо равна некоторой непрерывной функции 
, то площадь фигуры, ограниченной графиками данных функций и прямыми , , можно найти по формуле: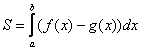 
4.если криволинейная трапеция ограничена кривой, заданной параметрически
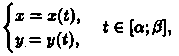
прямыми х = аих = bи осью Ох, то площадь ее находится по формуле
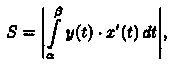
где а и β определяютсяиз равенств х(а) = а и х(β) =b.
5.площадь S криволинейного сектора, т. е. плоской фигуры, ограниченной непрерывной линией r=r(φ) и двумя лучами φ=а и φ=β (а < β), где r и φ — полярные координаты
