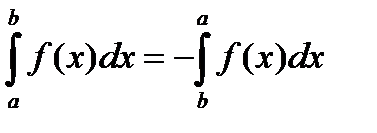Определённым интегралом от непрерывной функции f(x) на конечном отрезке [a, b] (где 
) называется приращение какой-нибудь её первообразной на этом отрезке. При этом употребляется запись 
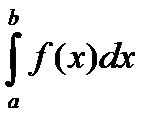
Числа a и b называются соответственно нижним и верхним пределами интегрирования, а отрезок [a, b] – отрезком интегрирования.
Таким образом, если F(x) – какая-нибудь первообразная функция для f(x), то, согласно определению,
Это равенство называется формулой Ньютона-Лейбница.
Свойства:
1. Определённый интеграл с одинаковыми пределами интегрирования равен нулю, т.е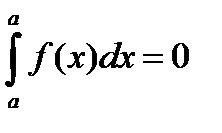 
2. Величина определённого интеграла не зависит от обозначения переменной интегрирования, т.е.
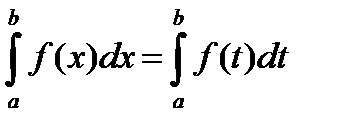
3. Постоянный множитель можно выносить за знак определённого интеграла, т.е.
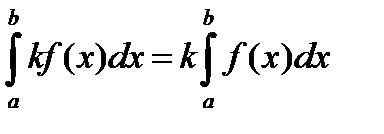
4. 
для интегрируемых на отрезке [a; b] функций y = f(x) и y = g(x)
5. Если отрезок интегрирования разбит на части, то определённый интеграл по всему отрезку равен сумме определённых интегралов по его частям, т.е. если 
, то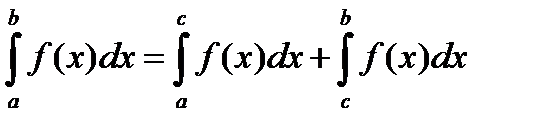 
6. При перестановке пределов интегрирования абсолютная величина определённого интеграла не меняется, а изменяется лишь его знак, т.е.
