Пусть в некоторой области 
задана функция 
и точка 
. Проведем из точки 
вектор 
направляющие косинусы которого 
. На векторе , на расстоянии 
от его начала рассмотрим точку 
, т.е. 
.
Будем предполагать, что функция и ее частные производные первого порядка непрерывны в области 
.Предел отношения 
при 
называется производной от функции 
в точке 
по направлению вектора и обозначается 
, т.е. 
.Для нахождения производной от функции 
в заданной точке 
по направлению вектора 
используют формулу: 
,
где 
– направляющие косинусы вектора 
, которые вычисляются по формулам:
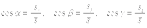.Пусть в каждой точке некоторой области 
задана функция 
.
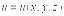Вектор, проекциями которого на оси координат являются значения частных производных этой функции в соответствующей точке, называется градиентом функции 
и обозначается 
или 
(читается «набла у»): 
.
При этом говорят, что в области определено векторное поле градиентов.
Для нахождения градиента функции 
в заданной точке используют формулу:
.
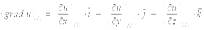