Прямая и плоскость
Три случая взаимного расположения прямой и плоскости в пространстве:
1. Прямая лежит в плоскости.
2. Прямая и плоскость имеют только одну общую точку (т.е. пересекаются).
3. Прямая и плоскость не имеют ни одной общей точки.
Прямая и плоскость называются параллельными, если они не имеют общих точек.
Признак параллельности прямой и плоскости:
Если прямая, не принадлежащая плоскости, параллельна какой-либо прямой, лежащей в этой плоскости, то она параллельно данной плоскости. См.Рис.1.
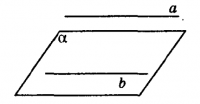
Рис.1
Свойство прямой, параллельной плоскости:
Если в одной из пересекающихся плоскостей лежит прямая, параллельная другой плоскости, то она параллельна линии пересечения плоскостей. См.Рис.2.
Рис.2
Плоскости
Параллельные плоскости – плоскости, не имеющие общих точек.
Признаки параллельности плоскостей:
§ Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны. См.Рис.3.
Рис.3
§ Если две плоскости перпендикулярны одной и той же прямой, то эти плоскости параллельны. См.Рис.4
Рис.4
Свойства параллельных плоскостей:
§ Если две параллельные плоскости пересекаются третьей плоскостью, то линии пересечения плоскостей параллельны. См.Рис.5
Рис.5
§ Отрезки параллельных прямых, заключенные между двумя параллельными плоскостями, равны. См.Рис.6
Рис.6