1) Вычислить сумму ряда:
· 
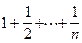(Ответ: при n=7, S=2,5929)
· 
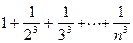(Ответ: при n=7, S=1,1932)
· 
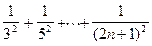(Ответ: при n=7, S=0,20249)
· 
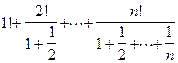(Ответ: при n=7, S=6,8478)
2) Вычислить: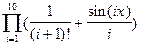 
3) Вычислить: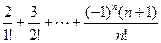 
4) Вычислить произведение ряда:
· 
;
· 
;
· 
.
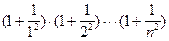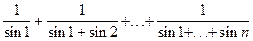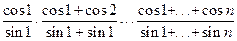5) Дано целое число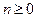 
. Проверить, что сумма ряда 
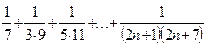не превышает дробь 
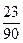. Вывести соответствующее сообщение.
6) Дано натуральное число x. Вычислить значение функции:
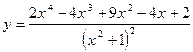на отрезке [2,3] с шагом 0.1.
7) Даны натуральные числа m и n. Вычислить: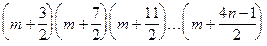 
. Проверить, что данное произведение больше 
.
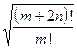8) Вычислить бесконечную сумму с заданной точностью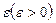 
. Считать, что требуемая точность достигнута, если вычислена сумма нескольких первых слагаемых и очередное слагаемое оказалось по модулю меньше, чем 
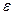. Это и все последующие слагаемые не учитывать. 
.
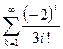9) Иррациональное число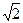 
можно разложить в цепную дробь следующим образом: 
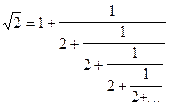. Дано положительное число 
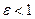. Выполнять процесс суммирования до тех пор, пока абсолютная величина разности между значением 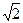, полученным с помощью функции SQR(x) и суммой дробей не станет меньше заданного 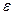. Вывести на экран полученное приближенное значение цепной дроби.
