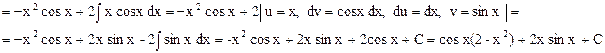1. Непосредственное интегрирование заключается в сведении данного интеграла к табличному интегралу.
Пример: 
.
2. Метод разложения заключается в использовании свойств линейности интеграла.
Пример: 
.
3. Интегрирование путём замены переменной
а) метод подведения под знак дифференциала, означает, что функция должна соответствовать дифференциалу: du = d(u + C)
, С ≠ 0 
.
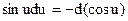
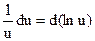
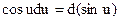
Пример: 
;
б) метод письменной замены переменной (подстановка) заключается в том, что x меняют на φ(t), где φ(t) – непрерывно дифференцируемая функция, и получают 
, причём после интегрирования возвращаются к старой переменной обратной подстановкой 
.
Примеры: 1) 
;
2) 
.
4. Интегрирование по частям заключается в использовании формулы 
, где u и v – дифференцируемые функции от x. Применение формулы необходимо в тех случаях, когда полученный интеграл будет проще исходного или когда он будет ему подобен. Этот метод используется для вычисления интегралов, представленных в виде двух сомножителей:
1. 
; 2 . 
; 3. 
;
4. 
; 5 . 
; 6. 
;
7. 
; 8. 
, где 
(x) – многочлен степени n.
В случаях 1–3 через u обозначают (x), в 4–7 – вторые сомножители, в 8 – любую функцию. А
оставшуюся часть подынтегрального выражения принимают в качестве dv.
Примеры:
1) 
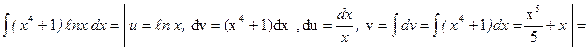
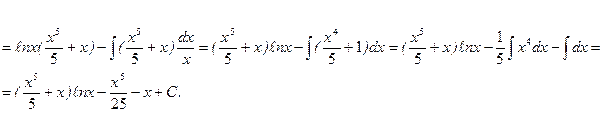
2) 
