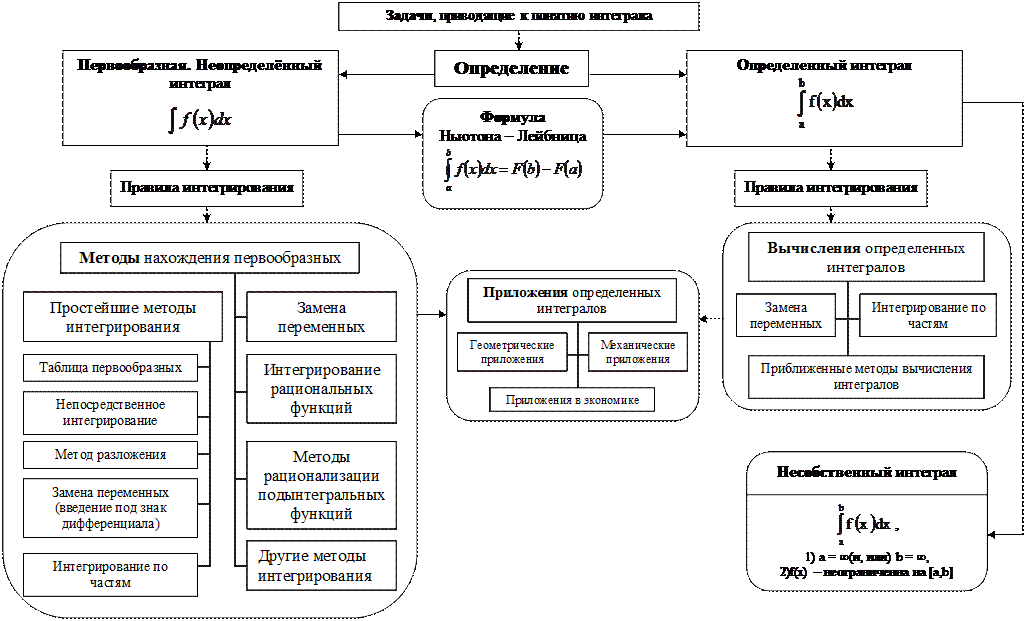
Структурно-логическая схема «Интеграл и его приложения»
НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
Первообразная
Функция F(x) называется первообразной функцией для функции f(x), или интегралом от f(x), если f(x) есть производная функции F(x), т. е. f(x)= F´(x).
Отыскание для данной произвольной функции её первообразной называется интегрированием (а весь комплекс вопросов связанных с этим – интегральным исчислением). Отыскание первообразной является обратной задачей для дифференцирования.
Прямая задача: Обратная задача:
дифференцирование интегрирование
f(x) →f´(x) f(x) = F´(x) → F(x)
Производная от числа равна нулю, т. е. (F(x)+С)´ = F´(x)= f(x). Поэтому общее выражение F(x)+С совокупности всех первообразных от функции f(x) называется неопределённым интегралом от этой функции и обозначается ∫f(x)dx = F(x)+С; произведение f(x)dx называется подынтегральным выражением, а f(x) – подынтегральной функцией, x – переменной интегрирования, ∫– знаком неопределённого интеграла.
Всякая непрерывная функция f(x) имеет бесчисленное множество различных первообразных функций, отличающихся друг от друга постоянным слагаемым.
Геометрически, в системе координат XOY, графики всех первообразных функций от данной функции f(x) представляют семейство кривых, зависящее от одного параметра C, которые получаются одна из другой путём параллельного сдвига вдоль оси OY. График каждой кривой называется интегральной кривой.
