При построении графикa вид функции, пределы, шаг изменения аргумента выбрать с использованием следующих данных.
| Вариант
| Функция
| Интервал задания,
шаг дискретизации
| |
|
|
| |
| y(t)=e-2tcos(20t)
| tÎ[0;1], Δt=0,01
| |
| y(t)=e-tsin2(10t)
| tÎ[0;1], Δt=0,01
| |
| y(t)=e-tsin3(20t)
| tÎ[0;1], Δt=0,01
| |
| y(t)=etcos(20t)
| tÎ[0;2], Δt=0,01
| |
| y(t)=etsin2(20t)
| tÎ[0;2], Δt=0,01
| |
| y(t)=etcos2(20t)
| tÎ[0;2], Δt=0,01
| |
| y(t)=etsin3(20t)
| tÎ[0;2], Δt=0,01
| |
| y(t)=√¯t¯ sin(10t)
| tÎ[0;4], Δt=0,02
| |
| y(t)=√¯t¯ sin(10t)
| tÎ[0;4], Δt=0,02
| |
| y(t)=tsin2(10t)
| tÎ[0;2], Δt=0,01
| |
| y(t)=(1-t)cos(20t)
| tÎ[0;2], Δt=0,01
| |
| y(t)=(1-e-t)cos(20t)
| tÎ[0;2], Δt=0,01
| |
| y(t)=sin2t sin(10t)
| tÎ[0;π], Δt=0,01
| |
| y(t)=cos2t sin(10t)
| tÎ[0;π], Δt=0,01
| |
| y(t)=(1+et)sin(20t)
| tÎ[0;2], Δt=0,01
|
Задание 12 (5.1.1) Построить в одном окне графики двух функций y1(t) и y2(t) с использованием команды plotyy(…)
При построении графиков вид функций, пределы, шаг изменения аргумента выбрать с использованием следующих данных.
| Вариант
| Функции
| Интервал задания,
шаг дискретизации
| |
|
|
| |
| y1(t)=10 , y2(t)=cos(20t) , y2(t)=cos(20t)
| t=[0;1], ∆t=0,01
| |
| y1(t)=10  , y2(t)= , y2(t)=  (10t) (10t)
| t=[0;1], ∆t=0,01
| |
| y1(t)=10  , y2(t)= , y2(t)=  (20t) (20t)
| t=[0;1], ∆t=0,01
| |
| y1(t)=10 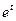 , y2(t)= cos(20t) , y2(t)= cos(20t)
| t=[0;1], ∆t=0,01
| |
| y1(t)=10 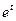 , y2(t)= , y2(t)=  (20t) (20t)
| t=[0;1], ∆t=0,01
| |
| y1(t)=10 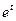 , y2(t)= , y2(t)=  (20t) (20t)
| t=[0;1], ∆t=0,01
| |
| y1(t)=10 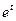 , y2(t)= , y2(t)=  (20t) (20t)
| t=[0;1], ∆t=0,01
| |
| y1(t)=10  , y2(t)=sin(10t) , y2(t)=sin(10t)
| t=[0;4], ∆t=0,02
| |
| y1(t)=10  , y2(t)=sin2(10t) , y2(t)=sin2(10t)
| t=[0;4], ∆t=0,02
| |
| y1(t)=10t, y2(t)=sin(10t)
| t=[0;2], ∆t=0,01
| |
| y 1(t)=10(1-t), y2(t)=cos(20t)
| t=[0;2], ∆t=0,01
| |
| y 1(t)=10(1-e-t), y2(t)=cos(20t)
| t=[0;2], ∆t=0,01
| |
| y1(t)=10sin2t, y2(t)=sin(10t)
| t=[0;  ], ∆t=0,01 ], ∆t=0,01
| |
| y1(t)=10cos2t, y2(t)=sin(10t)
| t=[0;  ], ∆t=0,01 ], ∆t=0,01
| |
| y1(t)=10(1+et), y2(t)=sin(20t)
| t=[0;2], ∆t=0,01
| Задание 13 (5.1.1) С помощью командыplot(t,y1,'S1′,t,y2,′S2′) построить в одном окне графики двух функций y1(t) и y2(t)
При построении графиков вид функций, пределы, шаг изменения аргумента и параметр ′S′выбрать с использованием следующих данных.
| Ва-ри-ант
| Функции, интервал задания,
шаг дискретизации
| Параметры (цвет линии, тип маркера, тип линии)
| |
|
|
| |
| y1(t)=  -0,5t, tÎ[0;2 -0,5t, tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Желтый, точка, сплошная
| y2(t)=cos(3t), tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Розовый, кружок, пунктирная
| |
| y1(t)=  , tÎ[0;2 , tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Голубой, крестик, штрих-пунктирная
| y2(t)=  (t), tÎ[0;2 (t), tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Красный, знак «плюс», штриховая
| |
| y1(t)=  , tÎ[0;2 , tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Зеленый, треугольник вершиной влево, сплошная
| y2(t)=  (t), tÎ[0;2 (t), tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Синий, треугольник вершиной вправо, пунктирная
| |
| y1(t)=0,05 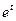 , tÎ[0;2 , tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Черный, пятиконечная звезда, штрих-пунктирная
| y2(t)= 60cos(2t),
tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Желтый, знак «плюс», штриховая
| |
| y1(t)=0,1 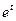 , tÎ[0;2 , tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Желтый, квадрат, штрих-пунтктирная
| y2(t)=60  (t),
tÎ[0;2 (t),
tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Розовый, ромб, штриховая
| |
| y1(t)=0,1 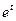 , tÎ[0;2 , tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Голубой, треугольник вершиной вниз, сплошная
| y2(t)=60  (2t),
tÎ[0;2 (2t),
tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Красный, треугольник вершиной вверх, пунктирная
| |
| y1(t)=0,1 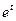 , tÎ[0;2 , tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Розовый, знак «плюс», пунктирная
| y2(t)= 60  (3t),
tÎ[0;2 (3t),
tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Голубой, пятиконечная звезда, штрих-пунктирная
| |
| y1(t)=  , tÎ[0;2 , tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Зеленый, шестиконечная звезда, штриховая
| y2(t)=2,5sin(t),
tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Желтый, точка, сплошная
| |
| y1(t)=  , tÎ[0;2 , tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Розовый, кружок, пунктирная
| y2(t)=2,5sin(t),
tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Голубой, крестик, штрих-пунктирная
| |
| y1(t)=t, tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Красный, знак «плюс», штриховая
| y2(t)=8sin(10t),
tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Зеленый, треугольник вершиной влево, сплошная
| |
| y1(t)=1-t, tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Синий, треугольник вершиной вправо, пунктирная
| y2(t)=6cos(t),
tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Черный, пятиконечная звезда, штрих-пунктирная
| |
| y1(t)=1-e-t, tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Желтый, знак «плюс», штриховая
| y2(t)=2cos(t), tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Красный, квадрат, штрих-пунтктирная
| |
| y1(t)=sin2t, tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Розовый, ромб, штриховая
| y2(t)=sin(10t),
tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Голубой, треугольник вершиной вниз, сплошная
| |
| y1(t)=cos2t,
tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Красный, треугольник вершиной вверх, пунктирная
| y2(t)=sin(t), tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Розовый, знак «плюс», пунктирная,
| |
| y1(t)=0,1(1+et),
tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Голубой, пятиконечная звезда, штрих-пунктирная
| y2(t)=60sin(t),
tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Зеленый, шестиконечная звезда, штриховая
|
Задание 14 (5.2.1) С помощью командыstem(t,y2,′S′) построить график функции y2(t)
При построении графиков вид функций, пределы, шаг изменения аргумента и параметр ′S′выбрать с использованием следующих данных.
| Вари-ант
| Функция, интервал задания,
шаг дискретизации
| Параметры (цвет линии, тип маркера, тип линии)
| |
|
|
| |
| y2(t)=cos(t), tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Розовый, кружок, пунктирная
| |
| y2(t)=  (t), tÎ[0;2 (t), tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Красный, знак «плюс», штриховая
| |
| y2(t)=  (t), tÎ[0;2 (t), tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Синий, треугольник вершиной вправо, пунктирная
| |
| y2(t)= 60cos(2t),
tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Зеленый, знак «плюс», штриховая
| |
| y2(t)= 60  (t),
tÎ[0;2 (t),
tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Розовый, ромб, штриховая
| |
| y2(t)= 60  (2∙t),
tÎ[0;2 (2∙t),
tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Красный, треугольник вершиной вверх, пунктирная
| |
| y2(t)= 60  (3t),
tÎ[0;2 (3t),
tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Голубой, пятиконечная звезда,
штрих-пунктирная
| |
| y2(t)=2,5sin(t),
tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Желтый, точка, сплошная
| |
| y2(t)=2,5sin(t),
tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Голубой, крестик, штрих-пунктирная
| |
| y2(t)=8sin(10t),
tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Зеленый, треугольник вершиной влево, сплошная
| |
| y2(t)=6cos(t), tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Черный, пятиконечная звезда, штрих-пунктирная
| |
| y2(t)=2cos(t), tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Красный, квадрат, штрих-пунтктирная
| |
| y2(t)=sin(10t),
tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Голубой, треугольник вершиной вниз, сплошная
| |
| y2(t)=sin(t), tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Розовый, знак «плюс», пунктирная,
| |
| y2(t)=60sin(t), tÎ[0;2  ], ∆t=0,2 ], ∆t=0,2
| Зеленый, шестиконечная звезда, штриховая
| | | | | |
Задание 15 (5.2.2) С помощью команды stairs(t,y1,′S′) построить график функции y1(t)
При построении графиков вид функций, пределы, шаг изменения аргумента и параметр ′S′ выбрать с использованием следующих данных.
| Вари-ант
| Функция,
интервал задания,
шаг дискретизации
| Параметры (цвет линии, тип маркера, тип линии)
| |
|
|
| |
| y1(t)=10  , tÎ[0;5], ∆t=0,2 , tÎ[0;5], ∆t=0,2
| Черный, треугольник вершиной вверх, сплошная
| |
| y1(t)= 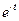 , tÎ[0;4], ∆t=0,2 , tÎ[0;4], ∆t=0,2
| Черный, шестиконечная звезда, пунктирная
| |
| y1(t)=  , tÎ[0;100], ∆t=5 , tÎ[0;100], ∆t=5
| Красный, ромб, штриховая
| |
| y1(t)=1-  , tÎ[0;5], ∆t=0,2 , tÎ[0;5], ∆t=0,2
| Черный, треугольник вершиной вверх, сплошная
| |
| y1(t)=  , tÎ[0;10], ∆t=0,6 , tÎ[0;10], ∆t=0,6
| Красный, кружок, штриховая
| |
| y1(t)=sin(t), tÎ[0;  ], ∆t=0,08 ], ∆t=0,08
| Зелёный, точка, сплошная
| |
| y1(t)= 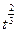 , tÎ[0;10], ∆t=0,6 , tÎ[0;10], ∆t=0,6
| Голубой, треугольник вершиной вверх, сплошная
| |
| y1(t)=  , tÎ[0,2;1], ∆t=0,06 , tÎ[0,2;1], ∆t=0,06
| Красный, треугольник вершиной вправо, пунктирная
| |
| y1(t)=arcsin(t), tÎ[0;1], ∆t=0,08
| Голубой, треугольник вершиной вправо, штриховая
| |
| y1(t)=arccos(t), tÎ[0;1], ∆t=0,06
| Зеленый, треугольник вершиной влево, сплошная
| |
| y1(t)=arctg(t), tÎ[0;5], ∆t=0,4
| Красный, ромб, пунктирная
| |
| y1(t)=arcctg(t), tÎ[0,1;5], ∆t=0,4
| Красный, квадрат, штрих-пунтктирная
| |
| y1(t)=arcsin(|t|), tÎ[-1;1], ∆t=0,08
| Красный, пятиконечная звезда, штриховая
| |
| y1(t)=arccos(|t|),
tÎ[-1;1], ∆t=0,08
| Синий, квадрат, штриховая
| |
| y1(t)=1-t  , tÎ[0;5], ∆t=0,35 , tÎ[0;5], ∆t=0,35
| Красный, пятиконечная звезда, штрих-пунктирная
|
Задание 16 (5.2.3) С помощью командыerrorbar(t,y,E,′S′)построить график функции y1(t)
При построении графиков вид функций, пределы, шаг изменения аргумента и параметр ′S′выбрать с использованием следующих данных.
| Вари-ант
| Функция, интервал задания,
интервал дискретизации
| Параметры (цвет линии, тип маркера, тип линии)
| |
| y1(t)=10  , tÎ[0;5], ∆t=0,3 , tÎ[0;5], ∆t=0,3
| Черный, треугольник вершиной вверх, сплошная
| |
| y1(t)= 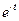 , tÎ[0;4], ∆t=0,2 , tÎ[0;4], ∆t=0,2
| Черный, шестиконечная звезда, пунктирная
| |
| y1(t)=  , tÎ[0;60], ∆t=4 , tÎ[0;60], ∆t=4
| Красный, ромб, штриховая
| |
| y1(t)=1-10 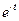 , tÎ[0;5], ∆t=0,3 , tÎ[0;5], ∆t=0,3
| Черный, треугольник вершиной вверх, сплошная
| |
| y1(t)=  , tÎ[0;5], ∆t=0,3 , tÎ[0;5], ∆t=0,3
| Красный, кружок, штриховая
| |
| y1(t)=2sin(t), tÎ[0;  ], ∆t=0,4 ], ∆t=0,4
| Зелёный, точка, сплошная
| |
| y1(t)= 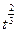 , tÎ[0;10], ∆t=0,6 , tÎ[0;10], ∆t=0,6
| Голубой, треугольник вершиной вверх, сплошная
| |
| y1(t)=  , tÎ[0;2,1], ∆t=0,06 , tÎ[0;2,1], ∆t=0,06
| Красный, треугольник вершиной вправо, пунктирная
| |
| y1(t)=3arcsin(t),
tÎ[0;1], ∆t=0,06
| Голубой, треугольник вершиной вправо, штриховая
| |
| y1(t)=4arccos(t),
tÎ[0;1], ∆t=0,06
| Зеленый, треугольник вершиной влево, сплошная
| |
| y1(t)=4arctg(t), tÎ[0;5], ∆t=0,3
| Красный, ромб, пунктирная
| |
| y1(t)=3arcctg(t),
tÎ[0.1;5], ∆t=0,4
| Красный, квадрат, штрих-пунтктирная
| |
| y1(t)=2arcsin(|t|),
tÎ[-1;1], ∆t=0,1
| Красный, пятиконечная звезда, штриховая
| |
| y1(t)=3arccos(|t|),
tÎ[-1;1], ∆t=0,12
| Синий, квадрат, штриховая
| |
| y1(t)=1-t  , tÎ[0;5], ∆t=0,3 , tÎ[0;5], ∆t=0,3
| Красный, пятиконечная звезда, штрих-пунктирная
|
Задание 17 (5.2.4) С помощью команд loglog(…), semilogx(…), semilogy(…) построить график функции y(t)
При построении графиков вид функций, пределы и шаг изменения аргумента выбрать с использованием следующих данных.
| Вариант
| Функция, интервал задания,
интервал дискретизации  
| Команда
| |
| y=30arctg3(t), tÎ[1; 1000], ∆t=1
| Loglog
| |
| y=(1-t) |sin(0,05t)cos(0,01t)| , tÎ[1; 1000], ∆t=1
| Semilogx
| |
| y=ln(t2)tg2(0,1t), tÎ[1; 1000], ∆t=1
| Semilogy
| |
| y=sin4(  ), tÎ[1; 1000], ∆t=1 ), tÎ[1; 1000], ∆t=1
| Loglog
| |
| y=0,01arctg2 (cos(0,03t)) , tÎ[1; 1000], ∆t=1
| Semilogx
| |
| y=tan(0,05sin2(0,1t)), tÎ[1; 300], ∆t=1
| Semilogy
| |
| y=ln(t)-cos2(  ), tÎ[1; 1000], ∆t=1 ), tÎ[1; 1000], ∆t=1
| Loglog
| |
| y=|arccos3(0,01t)|, tÎ[1; 1000], ∆t=1
| Semilogx
| |
| y=ln(t)-sin2(0,05t), tÎ[1; 1000], ∆t=1
| Semilogy
| |
| y=tg2(  ), tÎ[1; 1000], ∆t=1 ), tÎ[1; 1000], ∆t=1
| Loglog
| |
| y=(1000-t)cos(sin(0,05t)) , tÎ[1; 1000], ∆t=1
| semilogx
| |
| y=ln(cos2(15t))-  , tÎ[1; 1000], ∆t=1 , tÎ[1; 1000], ∆t=1
| Semilogy
| |
| y=(3-2·sin(0,1t))|sin(0,05t)| , tÎ[1; 1000], ∆t=1
| Loglog
| |
| y=ln(t)|sin(0,05t)| , tÎ[1; 1000], ∆t=1
| Semilogx
| |
| y=(1-t)|sin(0,05t)sin(0,05t)| , tÎ[1; 1000], ∆t=1
| Semilogy
|
Задание 18 (5.2.5) Построить график параметрической функцииy(x)с применением команды plot(…)
При построении использовать следующие данные.
| Вари-ант
| Функции
| Интервал задания,
интервал дискретизации
| |
| x(t)=sin(t), y(t)=cos3(t)
| tÎ[0; 2  ], ∆t=0,1 ], ∆t=0,1
| |
| x(t)=sin(t), y(t)=10·cos(t)
| tÎ[0; 2  ], ∆t=0,1 ], ∆t=0,1
| |
| x(t)=e  cos(10t), y(t)= e cos(10t), y(t)= e  sin(10t) sin(10t)
| tÎ[0; 2  ], ∆t=0,03 ], ∆t=0,03
| |
| x(t)=e  cos(10t), y(t)= e cos(10t), y(t)= e  sin(10t) sin(10t)
| tÎ[0;1], ∆t=0,03
| |
| x(t)=  cos(10t), y(t)=e cos(10t), y(t)=e  sin(10t) sin(10t)
| tÎ[0;1], ∆t=0,03
| |
| x(t)=  cos2(5t), y(t)=(1-t)sin(t) cos2(5t), y(t)=(1-t)sin(t)
| tÎ[0;1], ∆t=0,03
| |
| x(t)=  cos(t), y(t)=sin cos(t), y(t)=sin  (t)sin(10t) (t)sin(10t)
| tÎ[0;1], ∆t=0,03
| |
| x(t)=arctg(t)cos(10t), y(t)=sin2(t)sin(5t)
| tÎ[0;1], ∆t=0,03
| |
| x(t)=cos2(t)cos(10t), y(t)=sin2(t)sin(5t)
| tÎ[0;1], ∆t=0,03
| |
| x(t)=cos2(t)cos(10t), y(t)=sin2(t)sin(10t)
| tÎ[0;1], ∆t=0,03
| |
| x(t)=cos2(t)cos(cos(10t)), y(t)=sin2(t)sin(sin(10t))
| tÎ[0; 2  ], ∆t=0,01 ], ∆t=0,01
| |
| x(t)=sin2(t)cos(cos(10t)), y(t)=sin2(t)sin(sin(10t))
| tÎ[0; 2  ], ∆t=0,01 ], ∆t=0,01
| |
| x(t)=t2 cos(cos(5t)), y(t)=sin2(t)sin(sin(5t))
| tÎ[0; 2  ], ∆t=0,01 ], ∆t=0,01
| |
| x(t)=t2 cos(cos(5t)), y(t)=t2 sin(sin(5t))
| tÎ[0; 2  ], ∆t=0,01 ], ∆t=0,01
| |
| x(t)=t2 cos(cos(5t)), y(t)=t2 cos(sin(5t))
| tÎ[0; 2  ], ∆t=0,01 ], ∆t=0,01
|
|

 , y2(t)=cos(20t)
, y2(t)=cos(20t)
 , y2(t)=
, y2(t)=  (10t)
(10t)
 (20t)
(20t)
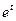 , y2(t)= cos(20t)
, y2(t)= cos(20t)
 (20t)
(20t)
 , y2(t)=sin(10t)
, y2(t)=sin(10t)
 ], ∆t=0,01
], ∆t=0,01
 -0,5t, tÎ[0;2
-0,5t, tÎ[0;2  , tÎ[0;5], ∆t=0,2
, tÎ[0;5], ∆t=0,2
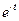 , tÎ[0;4], ∆t=0,2
, tÎ[0;4], ∆t=0,2
 , tÎ[0;5], ∆t=0,2
, tÎ[0;5], ∆t=0,2
 , tÎ[0;10], ∆t=0,6
, tÎ[0;10], ∆t=0,6
 ], ∆t=0,08
], ∆t=0,08
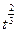 , tÎ[0;10], ∆t=0,6
, tÎ[0;10], ∆t=0,6
 , tÎ[0,2;1], ∆t=0,06
, tÎ[0,2;1], ∆t=0,06
 , tÎ[0;5], ∆t=0,35
, tÎ[0;5], ∆t=0,35

 cos(10t), y(t)= e
cos(10t), y(t)= e