Предположим, что некоторая функция f(x) задана таблицей своих значений:
| x
| x0
| x1
| …
| xn
|
| y
| y0
| y1
| …
| yn
|
Требуется найти интерполяционный полином Лагранжа – многочлен Ln(x) степени не выше n, значения которого в точках xk совпадают со значениями данной функции в этих точках, т.е. Ln(xk) = yk, k = 0,…, n.
Для нахождения интерполяционного полинома Лагранжа в Maple служит команда interp.
Пример:
Найти интерполяционный полином Лагранжа функции f(x)
Решение:
>> syms x
>> maple('interp([0,1,3,7],[5,4,2,1],x)')
ans =
1/56*x^3-1/14*x^2-53/56*x+5
Построим на рис. 7.7 узлы интерполяции (команда stem) и график найденного интерполяционного полинома Лагранжа
L3(x) = x3 - x2 - x+5:
>> stem([0 1 3 7],[5 4 2 1],'fill')
>> hold
Current plot held
>> ezplot(ans,-1, 8)
>>grid
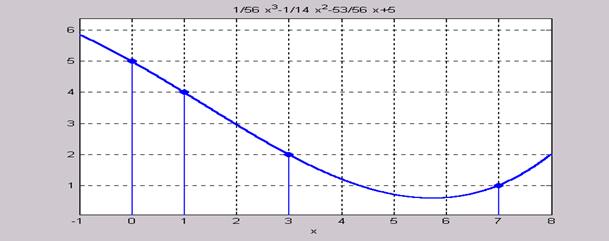
Рис. 7.7
Как видим из рис. 7.7, график найденного интерполяционного полинома Лагранжа проходит через узлы интерполирования