Поиск локального минимума функции одной переменной на некотором отрезке осуществляется командой fminbnd. Одна из модификаций fminbnd имеет вид fminbnd('file', x1,x2). Здесь
file – имя файл-функции, вычисляющей значение функции,
x1и x2 – границы отрезка изоляции локального минимума.
Первый входной аргумент можно задать как указатель на файл-функцию @»file. О других модификациях команды fminbnd можно узнать с помощью команды doc fminbnd.
Найти локальные минимумы функции e-xcos2πx на отрезке [0;2]. Создадим файл-функцию gr, вычисляющую значение функции e-xcos2πx при заданном значении аргумента x:
function y=gr(x)
y=exp(-x)*cos(2*pi*x);
Перед нахождением локальных минимумов построим график исследуемой функции командой fplot (рис. 6.3):
>> fplot(@gr,[0,2])
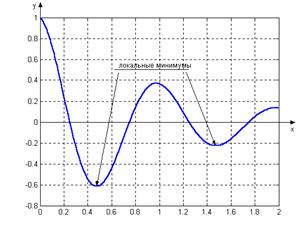
Рис. 6.3
На рис. 6.3 видно, что исследуемая функция имеет два локальных минимума. Вычислим значение х, при котором достигается второй локальный минимум:
>> x2=fminbnd(@gr,1.4,1.6)
x2 =
1.4749
Итак, второй локальный минимум достигается при х ≈ 1,4779.
Для одновременного вычисления значения функции в точке минимума следует вызвать fminbnd с двумя аргументами:
>> [x2,f]=fminbnd(@gr,1.4,1.6)
x2 =
1.4749
f =
-0.2260
Найдите самостоятельно остальные локальные минимумы и максимумы. Для нахождения локального максимума нет специальной функции, очевидно, что нужно искать минимум функции с обратным знаком.