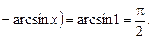Вычислить следующие несобственные интегралы первого рода или установить их расходимость:
9.57. 
; 9.58. 
;
9.59. 
; 9.60. 
;
9.61. 
; 9.62.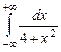 
.
Пусть функция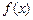 
определена во всех точках интервала 
кроме точки 
, 
– особая точка. Тогда рассматриваются пределы
и 
. (7)
Если пределы (7) существуют и конечны, то сумма этих пределов называется несобственным интегралом второго рода. Если же хотя бы один из пределов (7) не существует или равен бесконечности, то говорят, что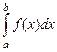 
– расходится.
Пример.
Вычислить несобственный интеграл или установить его расходимость
.
Решение.
Подынтегральная функция имеет разрыв в точке 
, поэтому 
