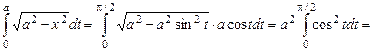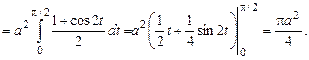2.1. Замена переменной. Если в определенном интеграле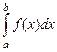 
мы переходим к новой переменной t по формуле 
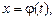то справедливо следующее равенство
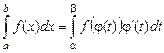. (4)
здесь 
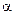и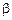 
– новые пределы интегрирования, которые находятся из условий: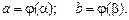 
Нахождение новых пределов – одна из особенностей применения формулы замены переменной в определенном интеграле (4). Другой особенностью является то, что в определенном интеграле в отличие от неопределенного не нужно переходить потом к старой переменной.
Пример.
Вычислить интеграл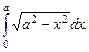 
.
Решение.
Введем замену переменных:
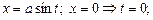
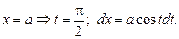
Тогда 
