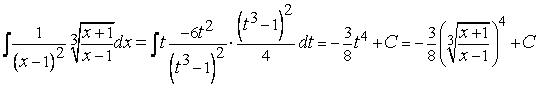Рассмотрим случаи, когда заменой переменной можно свести интегрирование нерациональных функций к интегрированию рациональных функций (т. е., как говорят, рационализировать интеграл).
Пусть 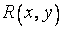 - рациональная функция своих аргументов
- рациональная функция своих аргументов 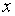 и
и 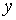 , т. е. над
, т. е. над 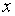 и
и 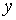 совершаются только арифметические операции, чтобы получить
совершаются только арифметические операции, чтобы получить 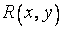 . Например,
. Например,
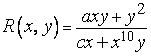 - рациональная функция, а
- рациональная функция, а
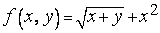 - не является рациональной.
- не является рациональной.
I. В ы ч и с л и т ь 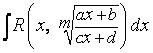 , где
, где 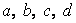 - постоянные числа,
- постоянные числа, 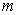 -натуральное число,
-натуральное число, 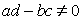 ,
, 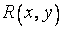 - рациональная функция.
- рациональная функция.
Функцию вида 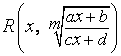 называют дробно-линейной иррациональностью.
называют дробно-линейной иррациональностью.
Покажем, что замена 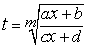 рационализирует интеграл. В самом деле,
рационализирует интеграл. В самом деле, 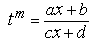 , откуда
, откуда 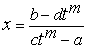 - рациональная функция от
- рациональная функция от 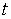 . Далее,
. Далее,
 .
.
Поэтому
 ,
,
где 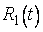 - рациональная функция по
- рациональная функция по 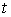 , интегрировать которую мы умеем.
, интегрировать которую мы умеем.
П р и м е р 1. Вычислить 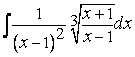 . Здесь
. Здесь 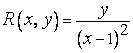 . Полагая
. Полагая 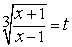 , получим
, получим 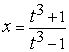 ,
,  ,
, 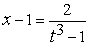 . Таким образом,
. Таким образом,