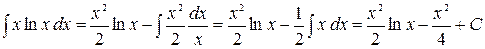Пусть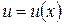 
и 
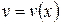- дифференцируемые функции. По свойству дифференциала:
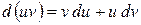
или
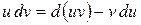
Интегрируя левую и правую части последнего равенства получаем:
.
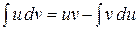Эта формула называется формулой интегрирования по частям для неопределенного интеграла.
Можно указать следующие типы интегралов, для нахождения которых используется формула интегрирования по частям:
1. 
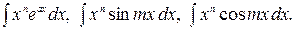
2. 
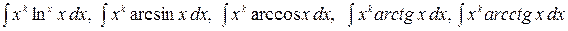
где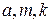 
- действительные числа 
, 
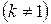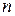- положительное число.
Для нахождения интегралов из первой группы формулу интегрирования по частям придется применить 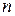раз (при первом применении полагают 
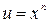, остальные сомножители подынтегрального выражения задают 
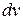), пока степень 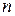переменной 
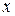не станет равной нулю, а сам интеграл табличным (см. пример ниже). Для нахождения интегралов второй группы полагают 
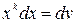(оставшиеся сомножители подынтегрального выражения задают выражение для 
).
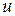На практике метод интегрирования по частям часто комбинируется с другими методами интегрирования.
Пример 10.6. Найти интегралы:
а)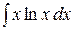 
б ) 
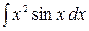в)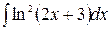 
РЕШЕНИЕ:
а) «Препятствием» к нахождению данного интеграла является присутствие сомножителя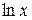 
в записи подынтегральной функции. Устранить его в данном случае можно интегрированием по частям. Полагаем 
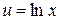, тогда 
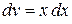. Тогда 
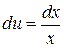и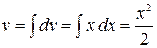 
. Используем формулу интегрирования по частям:
