Заменяющий символ градиента, V – объем, заключенный внутри поверхности А.

Поле температурного градиента является векторным, поэтому имеем:

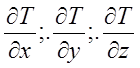где: и координаты

градиента и единичные векторы, имеющие направления координатных осей. За положительное принимается направление в сторону возрастания температуры: Тепловой поток – количество тепла Q, переданное в единицу времени. Тепловой поток, отнесенный к единице площади поверхности, называется плотностью теплового потока или тепловой нагрузкой поверхности нагрева. Вектор q всегда направлен в сторону, противоположную градиенту температур, так как самопроизвольно тепло передается только в сторону уменьшения температуры. Линии теплового потока – линии, касательные к которым совпадают с направлением вектора теплового потока (перпендикулярно к изотермическим поверхностям).

• Основной закон процесса теплопроводности сформулирован Фурье и поэтому носит его имя. Формулируется он следующим образом: плотность теплового потока пропорциональна градиенту температуры: Здесь коэффициент теплопроводности, Вт/мК.

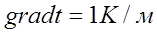По своему смыслу этот коэффициент численно равен тепловому потоку, проходящему через единицу поверхности 1 кв.м. при градиенте температуры, равном Знак минус в уравнении Фурье показывает, что теплота переносится

в сторону понижения температуры, приращение которой, в данном случае имеет отрицательное значение. Общее количество тепла, переданное теплопроводностью через стенку площадью поверхности, равной F, за время составит: Приведенное выше уравнение Фурье является математическим выражением закона теплопроводности. Количество тепла, передаваемое произвольным объемом внутри тела, можно найти путем интегрирования плотности теплового потока q по замкнутой поверхности А, ограничивающей этот объем так что: Здесь n – единичный вектор, нормальный к поверхности. Если

Использовать известные формулы из математики, тогда получаем следующие соотношения: По существу этим отражается первый закон термодинамики. Или после преобразований: и Окончательно имеем: общее уравнение теплопроводности в таких формах: или так: Здесь: коэффициент температуро - проводности (характеризует скорость переноса тепла в теле) имеет размерность: кв.м/сек. и комплекс оператор Лапласа. Приведенное выше уравнение

называют дифференциальным уравнением Фурье. Для тел неограниченных размеров в 2х направлениях (неограниченные по дине цилиндр или пластина) это уравнение становится одномерным и существенно упрощается, принимая такой вид: При условии отсутствия внутренних источников тепла (холода): При решении уравнений подобных уравнению теплопроводности необходимо также выполнение условий, которые из множества решений, отвечающих исходному уравнению, смогут найти единственное. Эти условия так и называются условиями ЕДИНСТВЕННОСТИ или условиями ОДНОЗНАЧНО

1) Геометрические условия, определяющие формы и размеры тел, участвующих в процессе;