Маршрут определяется как некоторая последовательность ребер, в котором граничные вершины двух соседних ребер совпадают, например, последовательность ребер 1, 4, 8, 6 – маршрут.
Маршрут, все ребра которого разложены, называется цепью, например, 5, 6, 4, 2.
Замкнутая цепь – это цепь возвращающаяся в ту же вершину, из которой начиналась и она называется циклом, например, 5, 7, 3.
Граф, любая пара вершин которого может быть соединена маршрутом, называется связным, например, 1-3 – связные.
Несвязный граф представляет собой совокупность отдельных частей (подграфов) называемых компонентами связности, например:
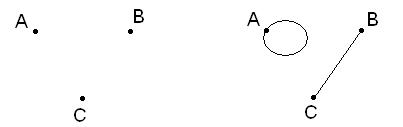
4) 5)
Связный граф не создающий циклов, называется деревом, например:
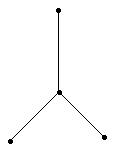
Дерево имеет n вершин, соединенных n-1 ребром.
Несвязный граф, компоненты которого являются деревьями, называется лесом, например:
