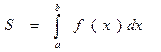Определенный интеграл

Введем понятие криволинейной трапеции. Рассмотрим функцию f(x), определенную на отрезке .Фигура, ограниченная линиями y=f(x), х=a, x=b, y=0 называется криволинейной трапецией.

y

f(a) y=f(x)

f(c₁)

f(x₁)

a=x₀ c₁ x₁ c₂ x₂ c₃ x₃ x_i-1 c_i x_i x_n-1 c_n x_n=b x

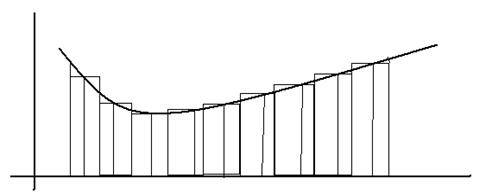
Решим задачу нахождения площади криволинейной трапеции, ограниченной линиями y=f(x), х=a, x=b, y=0 .

Разобьем на n равных частей точками х_i, тогда каждый из полученных отрезков будет равен 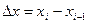, i=1,2…n.

Произвольным образом выберем в каждом отрезке по одной точке и обозначим их c_i. Проведем вертикальные линии x=x_i, тогда криволинейная трапеция разобьется на n частей , площадь каждой части будет приблизительно равна площади прямоугольника со сторонами f(c_i) и . А площадь криволинейной трапеции .

Сумма называется интегральной суммой функции f(x). Очевидно, что чем больше n, тем ближе значение интегральной суммы к значению площади криволинейной трапеции. Если существует предел 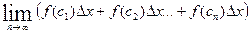и не зависит от выбора точек c_i, то функция называется интегрируемой, а указанный предел называется интегралом от функции f(x) на и обозначается

, где числа а и в называются соответственно нижним и верхним пределом интегрирования (читаются снизу вверх).

Следовательно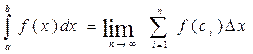

Тогда площадь криволинейной трапеции