Возможны три случая взаимного расположения прямой и плоскости:
– прямая и плоскость пересекаются, т.е. имеют одну общую точку;
– прямая и плоскость параллельны, т.е. не имеют общих точек;
– прямая лежит в плоскости, т.е. все точки прямой принадлежат плоскости.
Получим признаки для всех этих случаев. Пусть прямая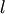 
и плоскость 
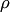заданы уравнениями:
т.е. прямая 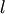проходит через точку 
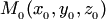коллинеарно вектору 
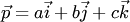а плоскость 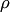перпендикулярна вектору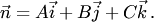 
Перечисленным выше случаям взаимного расположения прямой 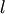и плоскости 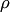соответствуют следующие признаки:
– прямая 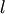и плоскость 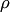пересекаются 
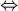векторы 
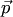и 
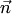не ортогональны (рис.4.37,а);
– прямая 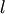и плоскость 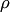параллельны 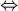векторы 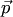и 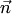ортогональны, а точка 
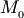не принадлежит плоскости 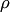(рис.4.37,б);
– прямая 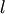лежит в плоскост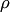и и 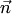векторы 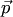и 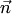ортогональны, а точка 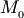принадлежит плоскости (рис.4.37,в).
Учитывая свойство скалярного произведения векторов получаем:
– прямая 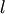и плоскость 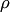пересекаются ;
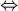– прямая 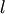и плоскость 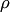параллельны
– прямая 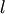лежит в плоскости
31. Дать определение окружности, записать ее геометрическое, каноническое и нормальное уравнения, изложить геометрические свойства.
