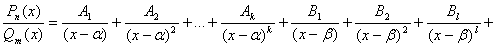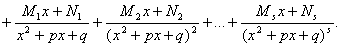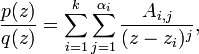Число a явл корнем многочлена p(x) тогда и только тогда, когда
p(x) делится без остатка на двучлен x − a (отсюда, в частности,
следует, что множество корней многочлена P(x) тождественно
множеству корней соответствующего уравнения P(x) = 0).
Свободный член многочлена делится на любой целый корень
многочлена с целыми коэффициентами (если старший
коэффициент равен 1, то все рациональные корни являются и целыми).
Пусть α — целый корень приведённого многочлена A(x) с целыми
коэффициентами. Тогда для любого целого k число A(k) делится на α-k.
6. Назвать виды простейших дробей и записать их формулы.
Изложить суть разложения рациональной дроби на сумму
простейших дробей.
6.Виды простейших дробей:
1) A/x-x0; A.x0 € R; (разделить/)
2) A/(x-x0)k; A,x0 € R k>=2; K€ N
3)Ax+B/x2+px+q, A,B,q,p € R; D<0
4)(Ax+B/(x2+px+q)r; r>=2, r€ N; D<0
Разложение прав рац. дроби на суму простейших дробей:
1)Если корень занменателя действ. то дробь раскладывается
на сумму дробей 1ого типа. 5/(x-1)(x+2)(x+4)=A1/x-1+A2/x+2+A3/x+4
2)Если в знаменателе дроби имеется кратный корень то он будет
представлен суммой простейших дробей 1ого и 2ого типов.
1/x6 = A1/x+A2/x2+…+A6/x6
3)Если в знаменатиле дроби имеентся квадратный корень с ДБ0
то ему будет соответствовать простейшая дробь 3 типа.
x+1/(x-1)(x2+2x+4)=A1/x-1 +Bx+C/x2+2x+4
4)Если в знаменателе имеется квадр трёхчлен в степени К. Д<0
то в разложении он будет представлен суммой дробей 3 и 4 порядка
7. Записать формулы представления рациональной дроби в
виде суммы простейших дробей с неопределенными коэффициентами.
Изложить метод неопределенных коэффициентов.
7.Правильную рациональную дробь 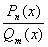 можно представить в виде
можно представить в виде
суммы конечного числа простейших рациональных дробей первого –
четвертого типов. Для разложения 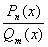 на простейшие дроби необходимо
на простейшие дроби необходимо
разложить знаменатель Qm(x) на линейные и квадратные множители, для
чего надо решить уравнение: 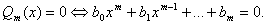
Теорема. Правильную рациональную дробь 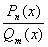 где
где
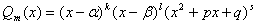 можно единственным образом
можно единственным образом
разложить на сумму простейших дробей:
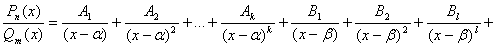
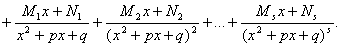
(A1, A2, …, Ak, B1, B2, …, B1, M1, N1, M2, M2, …, Ms, Ns – некоторые
действительные числа).
Метод неопределённых коэффициентов ― метод, используемый
в математике для нахождения искомой функции в виде точной или
приближённой линейной комбинации конечного или бесконечного
набора базовых функций. Указанная линейная комбинация берётся
с неизвестными коэффициентами, которые определяются тем или
иным способом из условий рассматриваемой задачи. Обычно для
них получается система алгебраических уравнений.
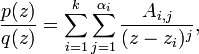
Метод неопредел коэффициентов.Суть метода неопределенных
коэффициентов состоит в следующем. Пусть дано разложение
правильной рациональной дроби
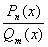 по формуле на простейшие дроби с неопределенными
по формуле на простейшие дроби с неопределенными
коэффициентами. Приведем простейшие дроби к общему знамен
Qm(x) и приравняем многочлен, получившийся в числителе,
многочлену Pn(x).Метод частных значений. При нахождении
неопределенных коэффициентов вместо того, чтобы сравнивать
коэффициенты при одинаковых степенях х, можно дать переменной
х несколько частных значений (по числу неопределенных
коэффициентов) и получить таким образом систему уравнений
относительно неопределенных коэффициентов. Особенно выгодно
применять этот метод в случае, корни знаменателя рациональной
дроби 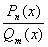 просты и действительны. Тогда оказывается удобным
просты и действительны. Тогда оказывается удобным
последовательно полагать равным каждому из корней знаменателя.
8.Дать понятие комплексного числа. Определить формы
представления комплексных чисел. Дать геометрическую
интерпретацию комплексного числа и его изображения на
комплексной плоскости, действительной и мнимой части
комплексного числа, его модуля и аргумента.
8. Комплексным числом Z наз. упорядоченная пара
действительных чисел
Алгебраическая форма:числа вида х + iy, где х и у —
действительные числа, а i — так называемая мнимая единица ,
x-действительная часть y-мнимая ... х + iy изображается точкой
плоскости, имеющей прямоугольные координаты х и у.
Рассмотрим плоскость с прямоугольной системой координат.
Каждому комплексному числу z=x+iy сопоставим точку плоскости
с координатами {x,y} (а также радиус-вектор, соединяющий
начало координат с этой точкой). Такая плоскость называется
комплексной. Вещественные числа на ней занимают горизонтал
ось, мнимая единица изображается единицей на вертикальной оси;
по этой причине горизонтальная и вертикальная оси называются

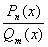 можно представить в виде
можно представить в виде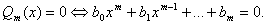
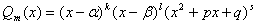 можно единственным образом
можно единственным образом