Пусть дано матричное уравнение AX = B, где A – квадратная матрица размерности n; B – матрица-столбец свободных членов размерности n×1; X – неизвестная матрица размерности n×1. Пусть A–невырожденная матрица (det(A) ≠ 0), тогда существует единственное решение этого уравнения. В матричной форме решение СЛАУ можно найти по формуле X = A−1B. Решение СЛАУ в матричной форме рассмотрим на примере.
Пример. Найти решение матричного уравнений AХ = В, где

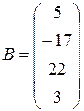
Сначала в среде Maxima зададим матрицы A и B:

Проверим существование и единственность решения:
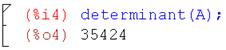
Матрица A невырожденная, значит, решение существует и единственно. Найдем его:
