Метод Крамера.

Другой метод решения системы линейных алгебраических уравнений основан на теореме Крамера.

Система из n уравнений с n неизвестными

(2.9)

в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:

x_i = D_i/D, (2.10)

где D = det A, а D_i – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов b_i.

D_i = .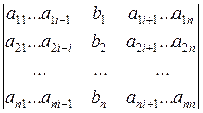

Формулы вычисления неизвестных (2.8) носят название формул Крамера. Таким образом, правило Крамера позволяет найти единственное решение системы (2.3) или сделать вывод о существовании бесконечного числа решений либо об их отсутствии:

1) Если 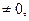система (2.3) имеет единственное решение, определяемое по формулам: .

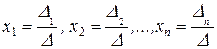2) Если 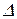= = 0, система имеет бесконечно много решений.

3) Если 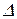= 0, а хотя бы один из 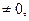система не имеет решений.

Если система однородна, т.е. b_i = 0, то при D¹0 система имеет единственное нулевое решение x₁ = x₂ = … = x_n = 0.

Пример. Найти решение системы уравнений: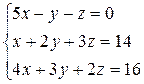

D = 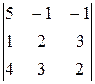= 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;

D₁ = = (28 – 48) – (42 – 32) = -20 – 10 = -30. x₁ = D₁/D = 1;

D₂ = = 5(28 – 48) – (16 – 56) = -100 + 40 = -60. x₂ = D₂/D = 2;

D₃ = 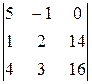= 5( 32 – 42) + (16 – 56) = -50 – 40 = -90. x₃ = D₃/D = 3.