Интегрирование некоторых иррациональностей.
Интегралы вида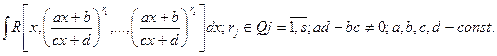 
Пусть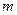 
- общий знаменатель чисел 
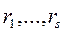.Тогда замена 
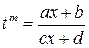приводит искомый интеграл к интегралу от рациональной функции.
Интегралы вида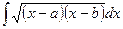 
приводят к интегралам предыдущего вида путем элементарного преобразования: 
.
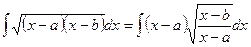Интегралы от дифференциального бинома. Подстановки Чебышева.
Выражение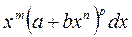 
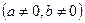называется дифференциальным биномом. Здесь 
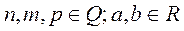. Замена 
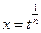приводит 
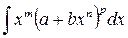к интегралу типа 
.
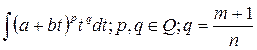П.Л. Чебышев показал, что данный интеграл выражается через элементарные функции только в трех случаях:
1. 
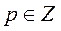замена: 
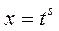, где 
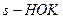знаменателей дробе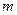й и 
.
2. 
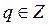замена: 
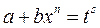, где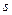 
знаменатель дроби 
.
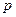3. 
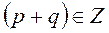замена: 
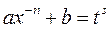, где 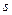знаменатель дроби .
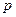Тригонометрические подстановки.
Интегралы вида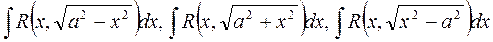 
приводятся к интегралам от рациональной относительно 
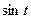и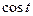 
функции с помощью надлежащей тригонометрической подстановки: для первого интеграла 
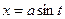(или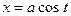 
), для второго 
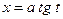(или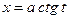 
) и для третьего 
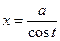(или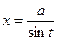 
).
Универсальная тригонометрическая подстановка.
Замена всех тригонометрических функций тангенсом половинного угла
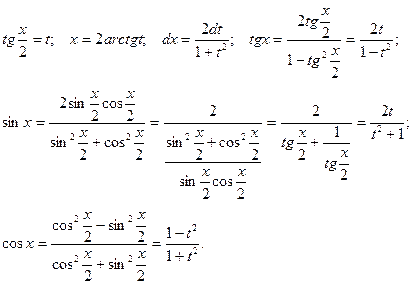
приводит интегралы вида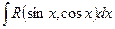 
к интегралам от рациональных функций.
