Интегралы вида
могут быть всегда приведены к интегралам от рациональных функций при помощи подстановки
При этом функции подынтегрального выражения выражаются через новые переменные
; 
; 
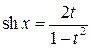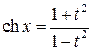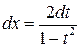
Примеры:
2.7.1. Найти интеграл: 
■ Применим формулу:
.
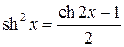Тогда первоначальный интеграл примет вид:
.◄
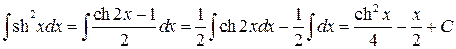2.7.2. Найти интеграл: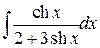 
■ Применим замену: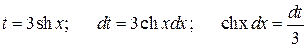 
.
.◄
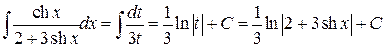2.7.3. Найти интеграл: 
■ Для решения применим формулу: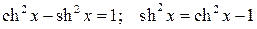 
. Тогда:
.
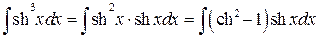Введём новую переменную:
.
Тогда первоначальный интеграл примет вид:
.◄
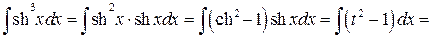
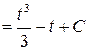2.7.4. Найти интеграл: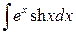 
■ Так как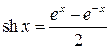 
, то Первоначальный интеграл примет вид:
.◄
2.7.5. Найти интеграл: 
■ Применим метод интегрирования по частям:
.
Тогда:
.◄
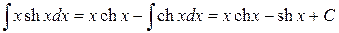2.7.6. Найти интеграл: 
■ Так как 
, то первоначальный интеграл примет вид:
. 
. ◄
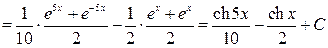В заключение отметим, что интегралы от трансцендентных функций часто не выражаются через элементарные функции. К таким интегралам относятся:
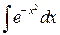- интеграл Пуассона;
и 
- и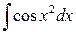нтегралы Френеля;
- интегральный логарифм;
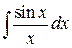- интегральный синус;
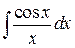- интегральный косинус.
