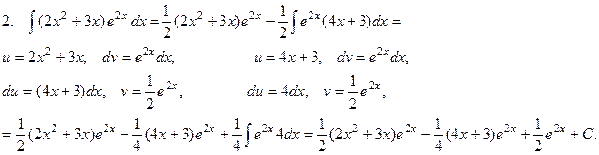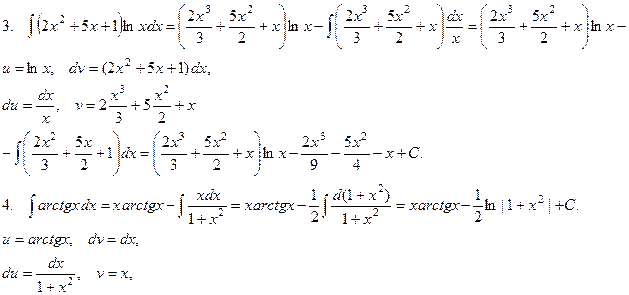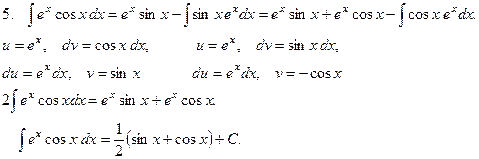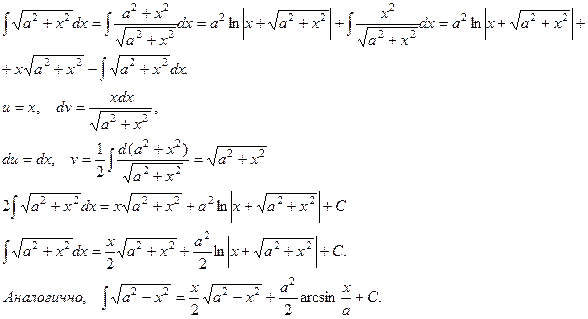Интегрирование по частям.

В интегрировании нет теоремы об интеграле произведения. В какой-то степени ее заменяет формула интегрирования по частям.

Пусть u и v - дифференцируемые функции х. Тогда

d(uv) = du v + u dv или udv = d(uv) – vdu

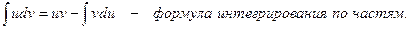
Формула интегрирования по частям применяется в следующих случаях:

1. 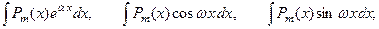где

P_m(x) = a₀x^m + a₁x^m-1 +….+ a_m-1 x + a_m,

u = P_m(x), dv = все остальное.

2.

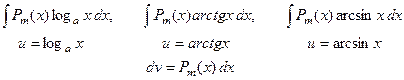
П р и м е р ы .

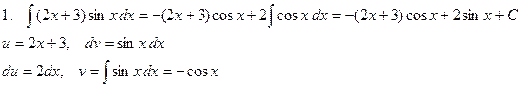
Иногда интегрирование по частям приходится применять несколько раз.