Пусть требуется найти интеграл 
непосредственное интегрирование, которого не дало окончательного результата.
Заменим переменную в подынтегральном выражении, положив 
, где 
непрерывная вместе со своей производной функция. Получим
.
Вычислим полученный интеграл по переменной 
, а затем после интегрирования по переменной перейдем к прежней переменной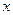 
, вновь воспользовавшись формулой
Например:
1. 
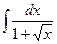
Сделаем замену переменной, положив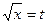 
, тогда интеграл примет вид
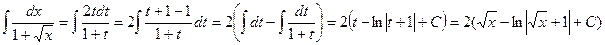
2. 
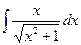
Положим 
, отсюда выразим 
и найдем 
Тогда 
3. 
Полагаем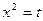 
, тогда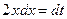 
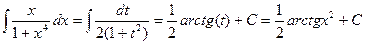
4. 
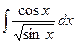
Положим 
тогда
Заметим, что подобрать нужную подстановку удается не всегда быстро, необходимы определенные навыки и практический опыт.
