1. 
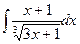
2. 
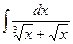
3. 
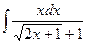
4. 
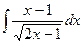
5. 
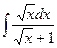
6. 
7. 
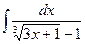
8. 
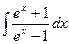
9. 
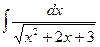
10. 
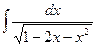
11. 
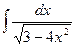
12. 
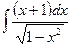
13. 
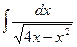
14. 
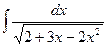
15. 
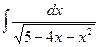
16. 
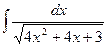
17. 
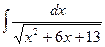
18. 
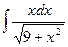
19. 
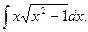
Интегрирование рациональных дробей.
Пункт 1. Рассмотрим интеграл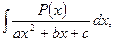 
где 
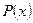- целый многочлен и а, в, с – постоянные 
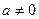. Если дробь неправильная, то делим 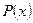на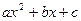 
, получаем в частном некоторый многочлен 
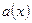и в остатке – линейный двучлен 
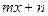, отсюда 
.
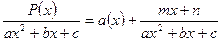Пример 1.
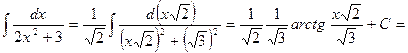
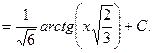
Пример 2.
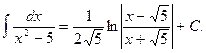
Пример 3.
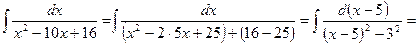
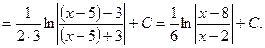
Пример 4. Найти интеграл: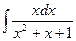 
.
Решение.
.
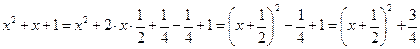
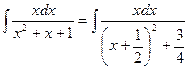Полагаем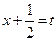 
, отсюда 
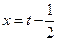и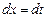 
.
Следовательно,
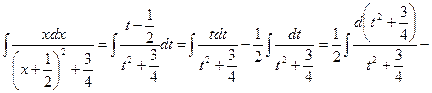
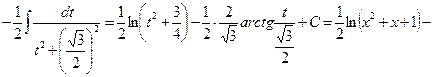
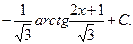
Пример 5. Найти интеграл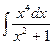 
.
Решение. Произведя деление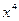 
на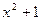 
, имеем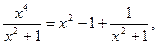 
отсюда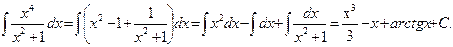 
Замечание. Если квадратный трехчлен 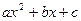имеет действительные и различные корн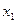и 
и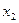 
, то для вычисления интеграла можно воспользоваться разложением подынтегральной функции на простейшие дроби:
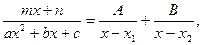(1)
где А и В – неопределенные коэффициенты. Числа А и В находятся путем приведения равенства (1) к целому виду и приравнивания коэффициентов при одинаковых степенях х в левой и правой частях полученного равенства.
Пример 6. Найти интеграл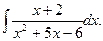 
Решение. Приравнивая знаменатель к нулю, получаем уравнение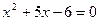 
; находим его корн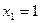и: 
и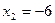 
.
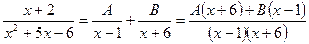
Отсюда, освобождаясь от знаменателя и учитывая, что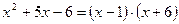 
, получим 
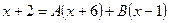, или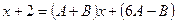 
.
Приравнивая друг к другу коэффициенты при одинаковых степенях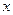 
в правой и в левой частях последнего равенства, будем иметь 
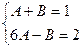. Следовательно, 
, 
.
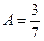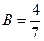Получаем 
