I.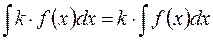 
.
II.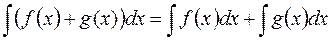 
.
III. Если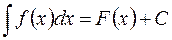 
, то 
.
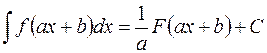Неопределенный интеграл – это множество функций и равенства I и II надо понимать как совпадение множеств. Например, равенство I означает следующее: чтобы получить элементы множества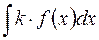 
, надо каждый элемент множества 
умножить на число 
. Правило III можно доказать так: 
. Тогда
,
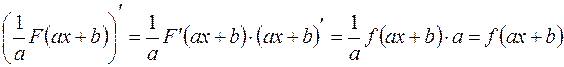т.е.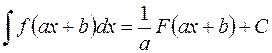 
.
Отметим, что правило III “работает” только тогда, когда вместо переменной интегрирования 
фигурирует линейная функция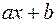 
:
,
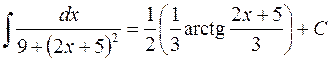но 
. Для этого интеграла правильный ответ имеет вид: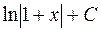 
.
Замечание. Правило III есть весьма частный случай замены переменной (см. следующий параграф).
