Определение. Пусть функция 
определена на промежутке 
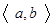, если на этом промежутке найдется дифференцируемая функция 
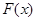, что для любого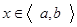 
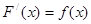, то функция 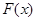называется первообразной для функции на .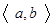
Пример.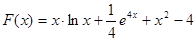 
на 
является первообразной для функции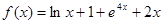 
.
Необходимо заметить, что общего понятия первообразной функции на любом множестве нет. Если промежуток 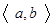содержит какой-либо конец, то 
и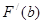 
- это соответственно односторонние левая и правая производные.
Теорема (об общем виде первообразной).
1. Пусть 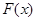- первообразная для функции на промежутке 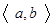и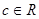 
, тогда функция 
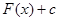тоже первообразная для на промежутке .
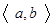2. Пусть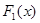 
и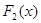 
являются первообразными для функции на промежутке 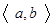, тогда найдется 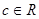, что для любого 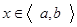выполняется равенство 
.
