Не все интегралы выражаются в элементарных функциях. Те интегралы, которые нельзя выразить в элементарных функциях, называются
неберущимися. Приведем основные примеры таких интегралов.
Например, 
– интеграл Пуассона, он широко используется в статистической физике, в теории теплопроводности и диффузии.
Интегралы Френеля 
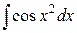и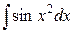 
широко применяются в оптике.
Часто встречаются в приложениях следующие интегралы:
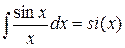– синус интегральный,
– косинус интегральный,
– интегральный логарифм.
Неберущимися являются также эллиптические интегралы. Они имеют вид
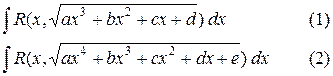
Покажем, что вычисление интеграла (1) сводится к вычислению
интеграла (2). Так как любой кубический многочлен с действительными коэффициентами имеет хотя бы один действительный корень 
, то его можно разложить на множители
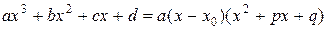. Тогда заменив 
, получим
.
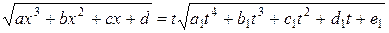Таким образом, вычисление эллиптического интеграла вида (1) сводится к вычислению эллиптического интеграла вида (2).
После некоторых преобразований вычисление интеграла (2) сводится к вычислению трёх интегралов
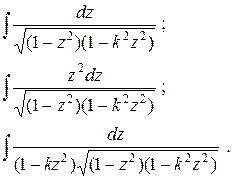
Они называются соответственно эллиптическими интегралами первого, второго и третьего родов.
Заменой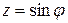 
эти интегралы сводятся к следующим:
;
;
.
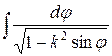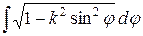Они называются эллиптическими интегралами первого, второго и третьего родов в форме Лежандра.
Для всех перечисленных интегралов составлены таблицы. Ввиду важности приложений эти функции изучены с такой же полнотой, как и простейшие элементарные функции.
