Задача.Найти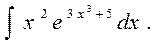 
Решение:
Обозначим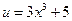 
. Тогда для дифференциала данной функции имеем выражение 
. Следовательно 
Подставляя в исходное выражение, получаем
.
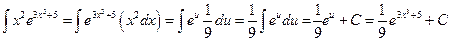Иногда не вводят обозначение для новой переменной, а все выражение для новой переменной через старую используют как ее имя, записывая это выражение под знаком дифференциала. Это и называют «подведением под знак дифференциала». В рассмотренном примере: 
, мы можем записать 
.
Задача.Найти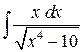 
.
Решение:
Обозначим 
. Тогда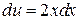 
. Следовательно, 
.
Получаем
.
Задача.Найти 
Решение:
Обозначим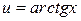 
. Тогда 
. Следовательно,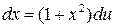 
.
Получаем
.
Вычисление интегралов вида 
.
Метод вычисления таких интегралов изложим на примере:
Задача.Найти 
Решение:
Выделим полный квадрат в знаменателе:
.
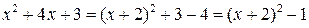Сделаем замену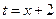 
. Тогда 
, 
.
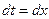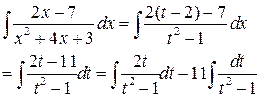
В первом интеграле сделаем замену: 
.
Тогда 
. Второй интеграл табличный.
Получаем:
Ответ: 
.
Задача.Найти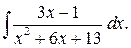 
Ответ: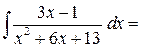 
.
Задача.Найти 
Ответ: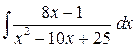 
= 
.
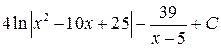Вычисление интегралов вида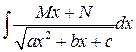 
.
Технология здесь аналогична рассмотренной в предыдущем случае.
Задача.Найти 
.
Решение:
Выделим полный квадрат в подкоренном выражении в знаменателе: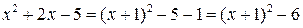 
, сделаем замену 
.
Получаем
В первом интеграле сделаем замену: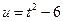 
.
Тогда 
. Второй интеграл табличный.
.
Ответ: 
.
Задача.Найти 
Указание:
Выделите полный квадрат в знаменателе: 
.
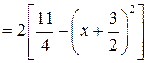Ответ: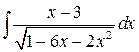 
.
