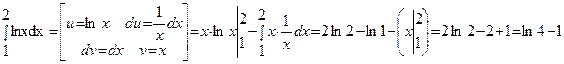II. Методы вычисления определенного интеграла.

1. Непосредственное интегрирование.

Пример .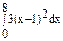

Решение. I способ.

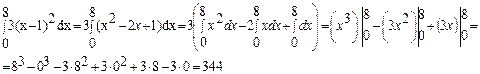
II способ.

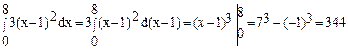
1. Замена переменной (интегрирование подстановкой).

Теорема Пусть выполняются следующие условия:

1. f(x) непрерывна на [a;b];

2. при изменении t от a до b j(t) принимает значения на отрезке [а;b], причем j(a)=а, j(b)=b;

3. j(t) непрерывна на [a;b]

Тогда имеет место формула: .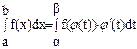

Пример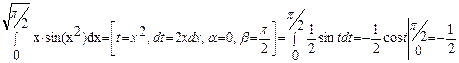

1. Интегрирование по частям в определенном интеграле.

Теорема Пусть функции u(x) и v(x) непрерывны и дифференцируемы на [a;b]. Тогда имеет место формула: .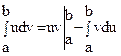

Пример