Рассмотрим общее уравнение плоскости:
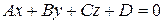 .
.
Равенство нулю отдельных коэффициентов в общем уравнении вносит особенности в расположение плоскости:
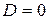 означает, что плоскость проходит через начало координат;
означает, что плоскость проходит через начало координат;
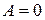 свидетельствует о том, что плоскость параллельна оси
свидетельствует о том, что плоскость параллельна оси 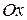 ;
;
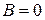 - параллельна оси
- параллельна оси 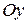 ;
;
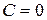 - параллельна оси
- параллельна оси 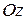 ;
;
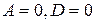 -плоскость проходит через ось
-плоскость проходит через ось 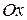 ;
;
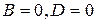 -плоскость проходит через ось
-плоскость проходит через ось 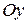 ;
;
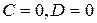 -плоскость проходит через ось
-плоскость проходит через ось 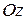 ;
;
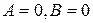 - плоскость параллельна плоскости
- плоскость параллельна плоскости 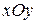 ;
;
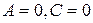 - плоскость параллельна плоскости
- плоскость параллельна плоскости 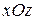 ;
;
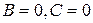 - плоскость параллельна плоскости
- плоскость параллельна плоскости 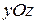 .
.
Пример 15.(Образец выполнения задачи 8 из контрольной работы). Построить плоскости
a)  ;
;
b) 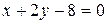 ;
;
c) 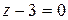 .
.
Решение. a) В этом уравнении ни один из коэффициентов не равен нулю. Отметим три точки, лежащие в данной плоскости (рис. 15):
M 





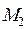
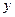
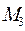
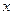
Рис. 15
если 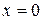 и
и 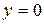 , то
, то 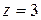 , т.е.
, т.е. 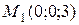 ;
;
если 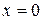 и
и 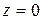 , то
, то 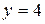 , т.е.
, т.е. 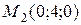 ;
;
если 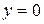 и
и 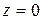 , то
, то 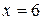 , т.е.
, т.е. 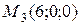 .
.
Теперь через эти точки проводим плоскость.
b) Т.к. в уравнении плоскости 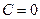 , то данная плоскость параллельна оси
, то данная плоскость параллельна оси 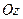 . Определим две точки, лежащие в данной плоскости:
. Определим две точки, лежащие в данной плоскости:
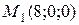 ,
, 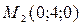 .
.
Через эти точки проводим прямую  , а через нее – плоскость параллельно оси
, а через нее – плоскость параллельно оси  (рис.16).
(рис.16).
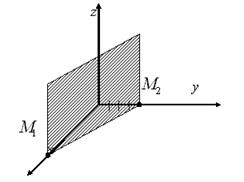
Рис. 16
c) В этом уравнении 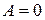 и
и 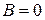 . Значит, данная плоскость параллельна плоскости
. Значит, данная плоскость параллельна плоскости 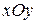 . Отметим точку, лежащую в данной плоскости:
. Отметим точку, лежащую в данной плоскости:
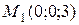 .
.
Проводим через нее плоскость параллельно плоскости  (рис.17). n
(рис.17). n 
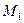




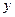
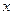
Рис. 17