Переходим к рассмотрению следующего типа дробей.
, 
, 
, 
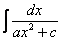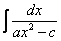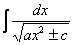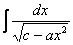(коэффициенты 
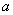и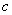 
не равны нулю).
На самом деле пара случаев с арксинусом и арктангенсом уже проскальзывала на уроке Метод замены переменной в неопределенном интеграле. Решаются такие примеры способом подведения функции под знак дифференциала и дальнейшим интегрированием с помощью таблицы. Вот еще типовые примеры с длинным и высоким логарифмом:
Пример 5
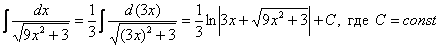
Пример 6
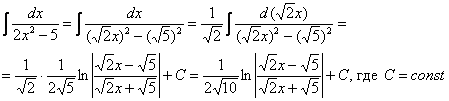
Тут целесообразно взять в руки таблицу интегралов и проследить, по каким формулам и как осуществляется превращение. Обратите внимание, как и зачем выделяются квадраты в данных примерах. В частности, в примере 6 сначала необходимо представить знаменатель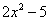 
в виде 
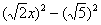, потом подвести 
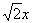под знак дифференциала. А сделать это всё нужно для того, чтобы воспользоваться стандартной табличной формулой 
.
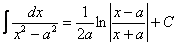Да что смотреть, попробуйте самостоятельно решить примеры №№7,8, тем более, они достаточно короткие:
Пример 7
Найти неопределенный интеграл:
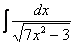
Пример 8
Найти неопределенный интеграл:
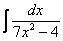
Если Вам удастся выполнить еще и проверку данных примеров, то большой респект – Ваши навыки дифференцирования на высоте.
