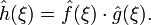Властивості

Визначення

Перетворення Фур'є функції 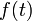математично визначається як комплексна функція 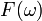, яка задається інтегралом

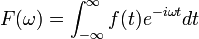
Обернене перетворення Фур'є задається виразом

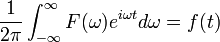
Властивості

Якщо задані інтегровні функції f(x), g(x) та h(x) та їхні відповідні перетворення Фур'є 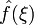, 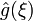та 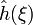, тоді самому перетворенню властиво наступне:

Лінійність

Для довільних комплексних чисел a та b, якщо h(x) = aƒ(x) + bg(x), тоді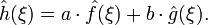  

Трансляція

Для довільного дійсного числа x₀, якщо h(x) = ƒ(x − x₀), тоді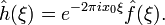 

Модуляція

Для довільного дійсного числа ξ₀, якщо h(x) = e^2πixξ₀ƒ(x), тоді  .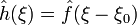

Масштабування

Для не рівного нулю дійсного числа a, якщо h(x) = ƒ(ax), тоді 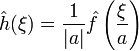 . Випадок a = −1 призводить до властивості "обернення часу", згідно з якою: якщоh(x) = ƒ(−x), тоді  .

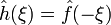Спряження

Якщо 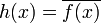, тоді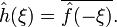 

Зокрема, якщо ƒ дійсне, тоді має місце "умова дійсності"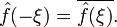  

Згортка

Якщо 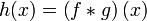, тоді