Интегралы вида
( 
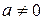), (5.1)
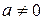( ) (5.2)
в зависимости от знака 
и знака дискриминанта квадратного трехчлена 
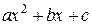приводятся путем выделения полного квадрата с последующей линейной заменой к табличным интегралам Т14 – Т17.
Замечание: Без ограничения общности всегда можно считать, что коэффициент 
равен единице по модулю.
Пример 1. Найти интеграл 
.
Решение: Выделим полный квадрат квадратного трехчлена 
. Тогда
.
Пример 2. Вычислить интеграл 
.
Решение: Выделяя полный квадрат квадратного трехчлена в знаменателе,
получим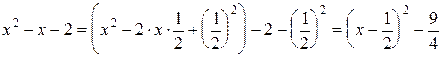 
. Тогда
.
Пример 3. Вычислить 
.
Решение: Выделение полного квадрата квадратного трехчлена дает 
. Тогда
.
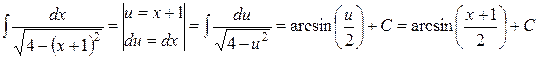Рассмотрим далее интегралы вида
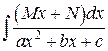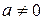( ), (5.3)
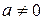( ). (5.4)
При вычислении интегралов (5.3), (5.4) сначала выделяют полный квадрат в квадратном трехчлене 
. Затем делают линейную замену, в результате чего исходный интеграл (5.3) или (5.4) можно разбить на два интеграла, один из которых является табличным интегралом Т14 – Т17, а другой находится методом замены переменной (знаменатель берется за новую переменную).
Пример 5.4. Найти интеграл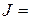 
.
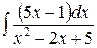Решение: Выделяем полный квадрат 
. Тогда
.
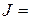
Полученный интеграл разбиваем на два интеграла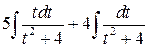 
. Второй интеграл является табличным: 
.
Первый интеграл вычисляем методом замены переменной
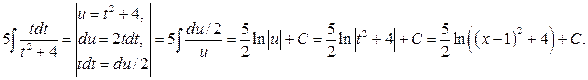
Итак, окончательно имеем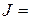 
.
