Пусть требуется вычислить неопределенный интеграл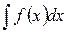 
. Введем новую переменную 
путем замены 
таким образом, чтобы функция 
была дифференцируемой и имела обратную функцию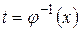 
. Далее, справедливой оказывается следующая формула:
, (3.1)
где интеграл справа может оказаться проще исходного интеграла. После вычисления интеграла справа следует вернуться к исходной переменной 
.
Пример 1. Вычислить интеграл 
.
Решение. Обозначим знаменатель подынтегральной функции буквой , т.е. введем сначала обратную функцию 
. Тогда 
, 
. Заметим, что 
. Применяем формулу (3.1):
где 
(введена новая произвольная постоянная).
