Алгоритм поиска глобального минимума методом сканирования.
1)Полагается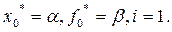 
2)Вычисляется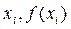 
3)Полагается оценка 
4)Проверяется условие окончания вычислений i=n. Если выполняется, то вычисления завершаются, если нет, то полагается i=i+1 и переход к пункту 2.
Ответ: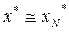 
,
.
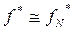Достоинство метода – простота алгоритма и независимость от вида функции.
Недостаток метода – очень большое количество вычислений (итераций).
Для того чтобы сделать алгоритм эффективным, необходимо знать дополнительную информацию о функции.
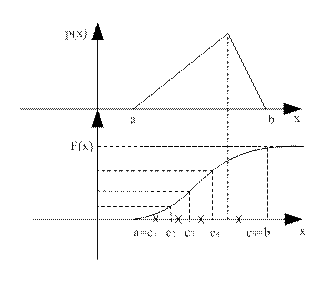
Пусть известна плотность распределения глобального минимума р(x) на отрезке а. Выберем отрезки так, чтобы была одинаковая вероятность попадания на отрезки.
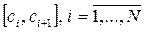- границы отрезка
- должны быть одинаковы и равны
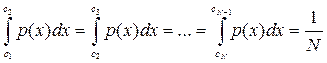
Проще всего решить эту задачу графически. Для этого построим функцию распределения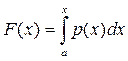
и рассечь ее прямыми параллельными оси абсцисс.
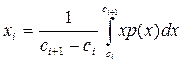
При поиске сначала выполняется n-раз процесс сканирования. На первом этапе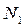 
- вычислений.
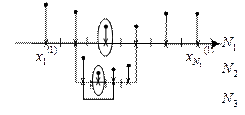
Находится минимальное значение функции. Затем рассматривается окрестность этой точки от границы до границы. Эта зона выделяется и затем на этом участке проводится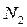 
вычислений. Такая процедура повторяется n-раз. (
)
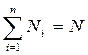1) 
, 
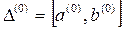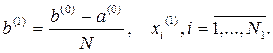
После проведения первого этапа получаем оценки:
,
.
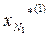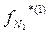Предположим, что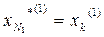 
.
2) 
, 
,
.
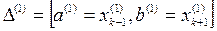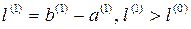
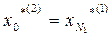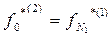Получаем после n-вычислений:
,
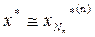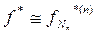
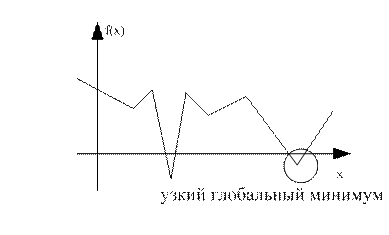
Недостаток метода: можно пропустить узкий глобальный минимум.
