Метод золотого сечения
Вычисления производятся и в случае, когда N задано и, когда N не задано. Идея та же, что и у метода Фибоначчи, но отличается правило выбора этих точек. Оно не зависит от количества вычислений.
Соотношение (2.8) используется и в методе золотого сечения.
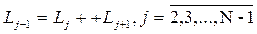(2.10)
Вместо (2.7) используем:
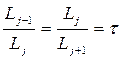(2.11)
,
,…,
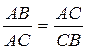
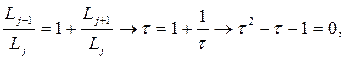
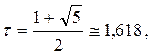
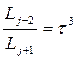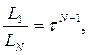
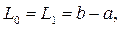
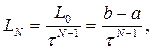
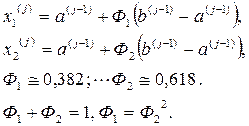
В отличие от метода Фибоначчи, в этом методе существует 2 условия окончания вычислений: либо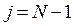 
, либо 
.
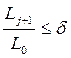Сравним эффективность метода Фибоначчи и метода золотого сечения.
Длины отрезка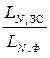 
. При больших N выполняется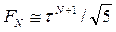 
Если пренебрегаем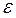 
, то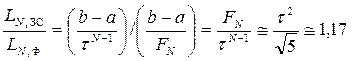 
.
Таким образом, мы видим, что метод золотого сечения на 17% больше дает длину отрезка (при больших N).
В отличие от предыдущих методов будем рассматривать многоэкстремальную функцию одной переменной.
Цель: найти точку глобального минимума.
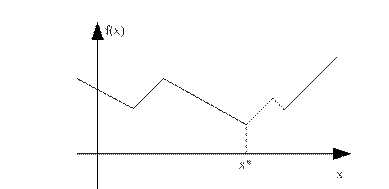
Задано: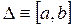 
, N – количество вычислений функции.
Найти: оценки 
2.5.1 Сканирование (метод перебора)
Отрезок 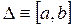разбивается на равные отрезки 
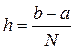и в середине этого отрезка берется точка 
.
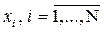Обозначим через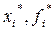 
соответственно оценки точки минимума и значения минимума, полученные после i-вычислений.
Кроме того, введем число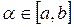 
и число 
.
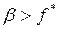