Унимодальные функции
ЧИСЛЕННЫЕ МЕТОДЫ ОДНОМЕРНОЙ ОПТИМИЗАЦИИ
Замечание: будем рассматривать только методы нулевого порядка
Унимодальные функции – это функции, которые на заданном отрезке имеют единственный экстремум.
Пусть 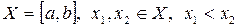 .
.
Функция f(x) называется унимодальной на Х, если существует такая точка 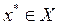 , что:
, что:
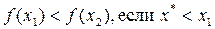
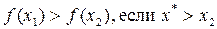
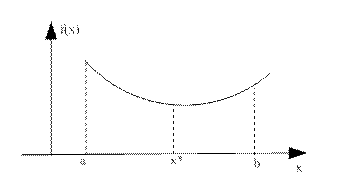
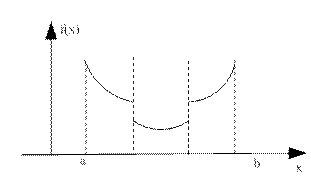
Свойство унимодальности помогает сформировать условие поиска минимума  .
.
Пусть f(x) унимодальна на Х, 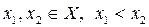 . Тогда, если:
. Тогда, если:
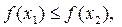 то
то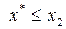
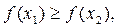 то
то 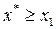 .
.
Таким образом, мы имея отрезок 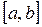 , после проведения вычислений, можем перейти к отрезку
, после проведения вычислений, можем перейти к отрезку 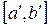 .
.
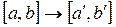

Говорят, что точка минимума локализована на отрезке 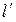 и отрезок называется отрезком локализации.
и отрезок называется отрезком локализации.
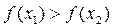
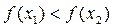
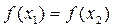
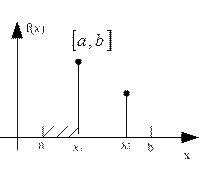
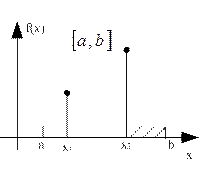
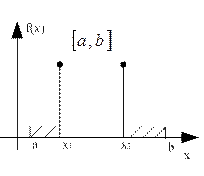
уменьшение длины отрезка локализации
Важным является понятие сходимость. Оттого как мы будем выбирать точки на отрезке, будет зависеть скорость сходимости.
Введем обозначения:
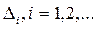 – отрезок локализации после i вычислений значений f(x).
– отрезок локализации после i вычислений значений f(x).
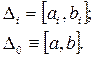 .
.
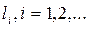 – длина отрезка локализации после i вычислений значений f(x).
– длина отрезка локализации после i вычислений значений f(x).
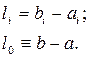
N – количество вычислений значений f(x)/
Рассмотрим случай, когда 


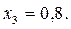
Возможны ситуации:
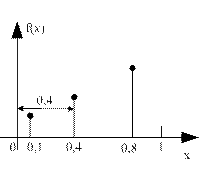

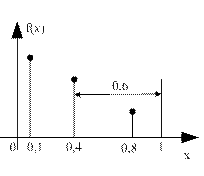
Пусть 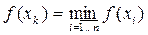 (i выбираем в качестве оценки минимума). Если это соотношение выполняется, то
(i выбираем в качестве оценки минимума). Если это соотношение выполняется, то 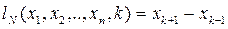
В качестве меры эффективности можно использовать максимальную длину отрезка локализации при данной стратегии выбора точек 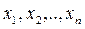 .
.
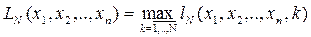
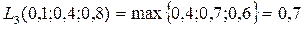
Теперь рассматривается задача выбора такой стратегии поиска 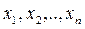 , которая приводила бы к минимальному значению критерия эффективности
, которая приводила бы к минимальному значению критерия эффективности 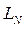 .
.
Каждый элемент дает минимальное значение максимума
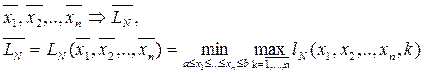 (2.1)
(2.1)