Необходимое условие локальной оптимальности
Пусть функции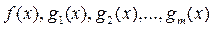 
дифференцируемы в точке 
. Если 
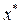точка локального минимума (локальное решение задачи (1.11)), то существует вектор 
, компоненты которого не равны нулю одновременно, такой что выполняется:
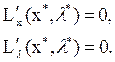(1.12)
При этом должны выполняться условия регулярности: градиенты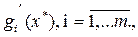 
должны быть линейно независимы. Это означает, что ранг матрицы 
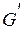, строками которого являются градиенты 
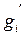, должен быть равен n, то есть должен быть отличен от нуля определитель хотя бы одной совокупности из m-столбцов этой матрицы.
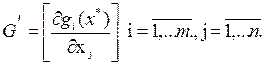
Точки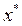 
удовлетворящие (1.12) также называются стационарными точками.
Метод множителей Лагранжа состоит из следующих этапов:
1.Составляется функция Лагранжа 
2.Находятся ее частные производные по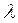 
3.Решается система вида (1.12) с m+n уравнений и m+n неизвестных.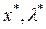 
считаются неизвестными. В результате находятся стационарные точки.
4.Для определения характера стационарных точек используется матрица Лагранжа.
Пусть функции 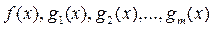дважды дифференцируемы в точке .
Предположим, что при некотором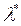 
выполняются условия (1.12), то есть 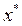стационарные точки и кроме того 
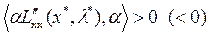при всех ненулевых 
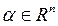таких, что 
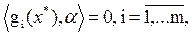тогда 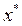– точка локального минимума (максимума) f(x) на множестве X.
Замечание: в дальнейшем мы будем рассматривать только необходимые условия, находить только стационарные точки и исследовать только выпуклые функции, а ля них стационарные точки и будут решением.
