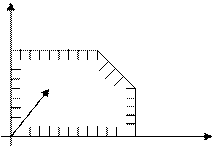
Графически решить ЗЛП можно только в том случае, если в системе ограничений и целевой функции имеется две независимые переменные х1, х2. Решением неравенства 
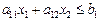является одна из двух полуплоскостей на которые вся плоскость делится прямой 
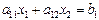. Таким образом, если система ограничений непротиворечива, то решением системы ограничений в случае двух переменных является выпуклый многоугольник (ограниченный или неограниченный). Оптимальное значение целевой функции находится в одной из вершин многоугольника (единственность решения), в том случае, когда оптимальному решению соответствует грань многоугольника решений , говорят что имеется множество оптимальных решений. Для нахождения оптимального решения целевой функции F необходимо построить вектор функции F, и строить линии уровня (перпендикуляры) к этому вектору. Та вершина, которую перпендикуляр пересечет первой, соответствует минимальному значению целевой функции, а которую последней – максимуму.
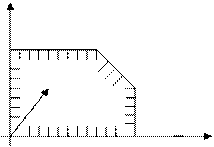х2
А В
С
О D х1
