Часто результатом случайного эксперимента является число. Например, можно подбросить игральную кость и получить одно из чисел: 1,2,3,4,5,6. Можно подъехать к бензоколонке и обнаружить определённое число автомашин в очереди. Можно выстрелить из пушки и измерить расстояние от места выстрела до места падения снаряда. В таких случаях будем говорить, что имеем дело со случайной величиной. Каждому исходу случайного эксперимента поставим в соответствие единственное число xk —значение случайной величины. Тогда естественно рассматривать случайную величину как функцию, заданную на множестве исходов случайного эксперимента. Случайная величина, которая может принимать лишь конечное или счётное число значений, называется дискретной.
Каждому значению xk случайной величины x можно поставить в соответствие вероятность рk = P(Ak) события Аk. Если такое соответствие определено то будем говорить, что задан закон распределения дискретной случайной величины Х. Обычно закон распределения дискретной случайной величины представляется в виде таблицы
| Х
| х1
| х2
| х3
| ¼
| хn
|
| P
| p1
| p2
| p3
| ¼
| pn
|
В дальнейшем для краткости будем называть величину pi вероятностью значения хi случайной величины. Отметим, что закон распределения содержит всю информацию о случайной величине, и задать случайную величину можно, просто представив её закон распределения.
Для закона распределения ДСВ соблюдается условие нормировки: 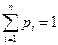 .
.