1.Если ряд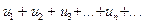 
сходится и имеет сумму S, то и ряд
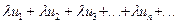(полученный умножением данного ряда на число l) также сходится и имеет сумму lS.
2.Если ряды 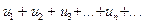и 
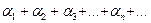сходится и
их суммы соответственно равны S1 и S2, то и ряд
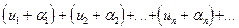(представляющий сумму данных рядов) также сходится, и его сумма равна S1+S2.
Свойства 1 и 2 непосредственно вытекают из свойств пределов числовых последовательностей.
3.Если ряд сходится, то сходится и ряд, полученный из данного путем отбрасывания (или приписывания) конечного числа членов.
Необходимый признак сходимости ряда:Если ряд сходится, то предел его
общего члена un при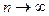 
равен нулю, т.е. 
.
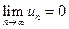Следствие: Если предел общего члена ряда un при 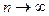не равен нулю, т.е.
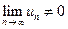, то ряд расходится.
